Aplicaciones de la optimización. Algoritmos para la eliminación de ruido

Contenidos

Método del gradiente para problemas sin restricciones.

Sea el problema de encontra un mínimo \(x^*\in\mathbb{R}^N\) de una función \(f:\mathbb{R}^N\to\mathbb{R}\). Es decir, resolver \[ \min_{x\in\mathbb{R}^N} f(x) \] El mínimo no tiene por qué ser único. En general, pueden existir varios mínimos locales. Sin embargo, si asumimos convexidad, el mínimo es único y los algoritmos basados en técnicas de descenso convergen al mínimo global.

El método más sencillo es el del gradiente o del descenso más pronunciado que para \(k=0,1,\ldots\) construye la sucesión \[ x^{(k+1)}=x^{(k)}- \tau \nabla f(x^{(k)}), \] siendo \(\tau\) el tamaño de paso. Tomaremos un \(x^{(0)}\) como valor inicial.

Un ejemplo general

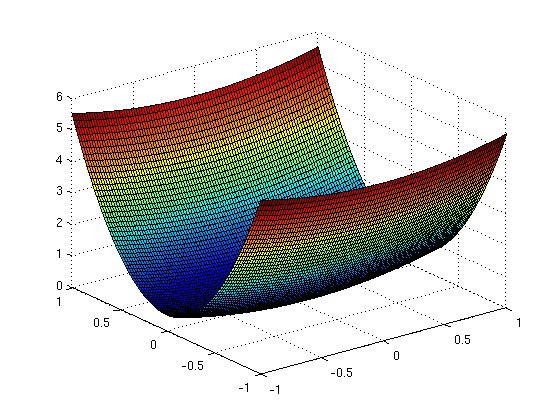
Sea la función convexa \(f(x)=\frac{1}{2}(x_1^2+\eta x_2^2)\) donde \(\eta>0\) es una constante. Esta función tiene un mínimo global en el origen \((x_1,x_2)=(0,0)\).

Para aplicar el método del gradiente, empezamos fijando \(\eta\) y definiendo \(f\).

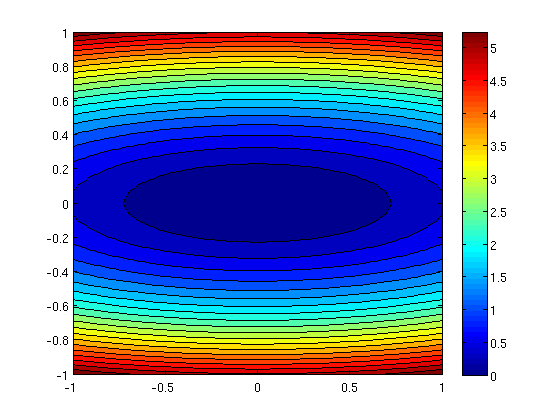
eta=10;                                 % definimos eta
f = @(x1,x2)(x1.^2+eta*x2.^2)/2;        % definimos la función
[u,v] = meshgrid(-1:0.02:1,-1:0.02:1);  % calculamos variables para dibujar f
F=f(u,v);
figure,surf(u,v,F)                      % representación de f como superfície
figure,contourf(u,v,F,20);              % representación de f con curvas de nivel
colorbar

Implementamos el método del gradiente. Calculamos el gradiente analíticamente y lo definimos.

Gradf = @(x)[x(1); eta*x(2)];   % definimos el gradiente
tau = 1.8/eta;                  % definimos el tamaño de paso
x=[0.5,0.5]';                   % valor inicial
X=x;                            % inicializamos la sucesión
for k=1:20                      % construímos la sucesión
     x=x-tau*Gradf(x);
     X=[X x];
end

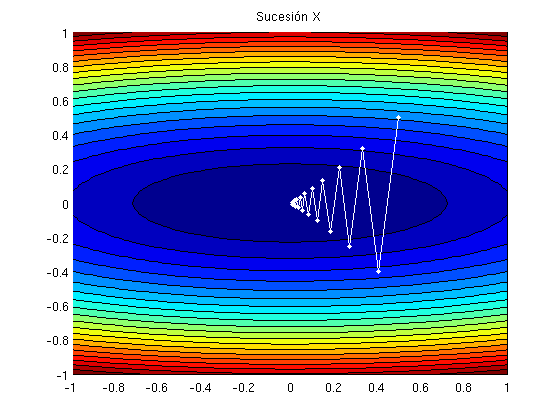
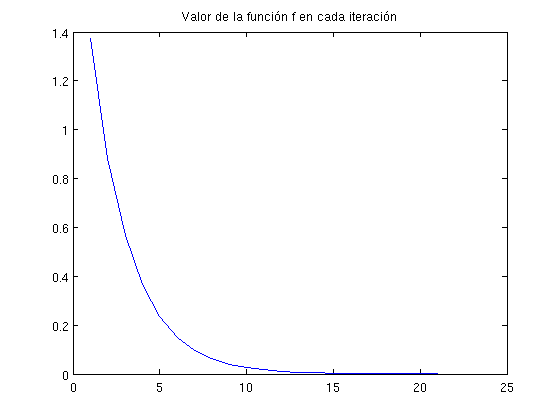
En dos gráficas podemos ver el camino que sigue la sucesión X y cómo \(f(x^{(k)})\) va disminuyendo.

figure, hold on
contourf(u,v,F,20)              % representación función f
plot(X(1,:), X(2,:), 'w.-')     % representación sucesión X
title('Sucesión X')
hold off
f_descenso=f(X(1,:),X(2,:));    % cálculo de f para los puntos de X
figure,plot(f_descenso)         % representación
title('Valor de la función f en cada iteración')

Eliminación de ruido en imágenes

En lugar de minimizar una función \(f:\mathbb{R}^N\to\mathbb{R}\) utilizando una sucesión de puntos \(x^{(k)}\in\mathbb{R}^N\), vamos a minimizar un funcional \(J:V\to\mathbb{R}\) donde \(V\) es el espacio de imágenes (un espacio de funciones continuamente diferenciables) utilizando una sucesión de imágenes \(u^{(k)}(x)\).

El funcional \(J\) se obtiene sumando dos términos, \(J=J_1+\lambda J_2\). El primer término es el término de fidelidad que obliga a que la imagen final no sea muy distinta de la imagen inicial. El segundo término es el término de regularización que utilizamos para realizar la eliminación de ruido.

Una elección habitual del término de fidelidad es el funcional convexo \[J_1(u)=\frac{1}{2} \|u-u_0\|^2= \frac{1}{2}\int_{\Omega}|u(x)-u_0(x)|^2dx\] donde \(\Omega\) es el conjunto de pixels y \(u_0\) es la imagen inicial.

Como término de regularización utilizamos \[J_2(u)=\frac{1}{2} \|\nabla u\|^2= \frac{1}{2}\int_{\Omega}|\nabla u(x)|^2dx\] que también es convexo.

El problema a resolver es: encontrar un mínimo \(u^*\in V\) de \(J:V\to\mathbb{R}\), es decir, resolver \[ \min_{u\in V} \frac{1}{2}\int_{\Omega}|u(x)-u_0(x)|^2dx+ \lambda\frac{1}{2}\int_{\Omega}|\nabla u(x)|^2dx .\] Aquí, \(\lambda>0\) es un parámetro que controla la relación entre la fidelidad y la regularización.

Para usar el método del gradiente necesitamos el gradiente de \(J\), que es \[ \nabla J(u(x))= u(x)-u_0(x) -\lambda\Delta u(x) .\] Entonces, aplicando el algotimo obtenemos \[ u^{(k+1)}(x)=u^{(k)}(x)-\tau \big( u^{(k)}(x)-u_0(x) -\lambda\Delta u^{(k)}(x) \big) \]

Ejemplo Si utilizamos la imagen cameraman.tif

clear
I=imread('cameraman.tif');

Primero transformamos de formato sin signo entero de 8 bits a punto flotante de doble precisión, le añadimos ruido y la normalizamos para que los valores de la intensidad vuelvan a estar en \([0,1]\).

u0=im2double(I);
u0=u0+0.05*randn(size(u0));
u0=(u0-min(min(u0)))/(max(max(u0))-min(min(u0)));

Definimos el paso inicial y calculamos la sucesión, renormalizando la imagen en cada iteración. Además, tenemos en cuenta que \[\Delta u=\mathrm{div}\left(\nabla u\right)\]

tau=0.1;
lambda=2;
u=u0;
for k=1:20
    [ux,uy]=gradient(u);
    u=u-tau*(u-u0-lambda*divergence(ux,uy));
    u=(u-min(min(u)))/(max(max(u))-min(min(u)));
end
figure,imshow(u0)
figure,imshow(u)

Ejercicio 1. La cantidad de error relativo añadido a la imagen sin ruido es aproximadamente \(5\%\). Calcular la diferencia relativa entre \(u_0\) y \(u\) para distintos valores de \(\tau\), por ejemplo \(\tau=0:0.025:0.1\) y dibuja el resultado. Visualmente, qué \(\tau\) es mejor para eliminar el ruido.

Ejercicio1

La diferencia relativa entre u y u0 para tau=0.000 es del   0.00%
La diferencia relativa entre u y u0 para tau=0.025 es del   5.04%
La diferencia relativa entre u y u0 para tau=0.050 es del   6.33%
La diferencia relativa entre u y u0 para tau=0.075 es del  16.46%
La diferencia relativa entre u y u0 para tau=0.100 es del  21.88%

Ejercicio 2. Usar un criterio de parada que utilice la diferencia relativa entre dos iteraciones sucesivas.

Por ejemplo, utilizando tol=0.01 y la norma euclidea

Ejercicio2

Ejercicio 3. Si utilizamos como \(J_2\) \[ J_2(u) = \int_\Omega \|\nabla u(x)\| dx .\] Su gradiente es \[ \nabla J_2(u) = \mathrm{div}\left(\frac{\nabla u(x)}{\|\nabla u(x)\|}\right). \] Como en las regiones donde \(\nabla u(x) =0\) el valor \(\nabla J_2(u)\) no está definido, haremos la siguiente aproximación \[ \nabla J_{2\epsilon}(u) = \mathrm{div}\left(\frac{\nabla u(x)}{\sqrt{\epsilon^2+\|\nabla u(x)\|^2}}\right). \] Usa los siguientes parámetros en tu programa: \(\lambda=0.1\), \(\tau=0.1\), \(\epsilon=0.001\).

Ejercicio3

Se puede observar la imagen resultante está menos borrosa y que, en general, la eliminación de ruido ha mejorado.