Derivación numérica

Contenidos

Derivada primera de funciones de una variable

Buscamos obtener una aproximación de $f'$ en un punto $\hat x$ en función de valores de $f$ en un número finito de puntos cercanos a $\hat x$.

¿Por qué?

  • Porque sólo conocemos los valores de $f$ en un número finito de puntos $x$.
  • Porque es menos costoso calcular la aproximación que el valor exacto.

A partir de la definición de derivada

$$ f'(\hat x)=\lim_{h\to0}\frac{f(\hat x+h)-f(\hat x)}{h} $$

podemos obtener tres aproximaciones o fórmulas en diferencias finitas

Diferencias finitas progresivas

$$ (\delta^+ f)(\hat x)=\frac{f(\hat x+h)-f(\hat x)}{h}$$

Diferencias finitas regresivas

$$ (\delta^- f)(\hat x)=\frac{f(\hat x)-f(\hat x -h)}{h}$$

Diferencias finitas centradas

$$ (\delta f)(\hat x)=\frac{1}{2}\big((\delta^+ f)(\hat x)+(\delta^- f)(\hat x)\big)= \frac{f(\hat x+h)-f(\hat x-h)}{2h}$$

Tener en cuenta que si solo usamos una de estas fórmulas no podemos calcular la derivada al menos en un extremo del intervalo. Por ejemplo, si usamos la fórmula progresiva no podemos calcular $(\delta^+ % f)(b)$ porque necesitamos $f(b+h)$ que, en general, es desconocido.

Órdenes python Para los ejecicios propuestos es útil la orden np.diff(x) que calcula $(x_2-x_1,x_3-x_2,\ldots,x_n-x_{n-1})$, y la orden np.linalg.norm(x) que calcula la norma euclídea de un vector $x$, por ejemplo

$$ \text{norm}(x)=\sqrt{\sum_{i=1}^n x_i^2}$$

Ejercicio 1

Dada la función $f(x)=e^x$ en $[h,1-h]$ y para h=0.1 y h=0.01.

  • Calcular y dibujar su derivada exacta.
  • Calcular y dibujar, sobre la figura anterior, su derivada aproximada usando diferencias finitas progresivas, df_p, regresivas, df_r, y centradas, df_c.
  • Calcular y dibujar, en una figura nueva, el error en cada punto para cada una de las aproximaciones, $f'(x_i)-df_a(x_i)$, donde $x_i$ son los puntos y $a=p,~r$ o $c$.
  • Calcular el error global relativo de cada aproximación usando np.linalg.norm(x) y la fórmula
$$ Error_{Global\,rel}=\sqrt{\frac{\sum_{i=1}^n (f'(x_i)-df_a(x_i))^2}{\sum_{i=1}^n (f'(x_i))^2}}.$$
In [1]:
%matplotlib inline
from __future__ import division
import numpy as np
import matplotlib.pyplot as plt
In [2]:
%run'Ejercicio1.py'

h            E(df_p)          E(df_r)        E(df_c) 

0.100	 5.170918e-02	 4.837418e-02	 1.667500e-03


h            E(df_p)          E(df_r)        E(df_c) 

0.010	 5.016708e-03	 4.983375e-03	 1.666675e-05

Vemos que la fórmula centrada da lugar a un error menor. Esto se debe a que las fórmulas progresiva y regresiva son de orden 1 y la fórmula centrada es de orden 2.

¿Es posible conseguir aproximaciones de orden 2 para $f'(a)$ y $f'(b)$? Si usamos un polinomio de interpolación de $f$ de $2^{o}$ grado en $x_{0}$, $x_{1}$, $x_{2}$, siendo $y_{j}=f(x_{j})$, el polinomio de interpolación en la forma de Newton es:

$$ p(x)=[y_{0}]+[y_{0},y_{1}](x-x_{0})+[y_{0},y_{1},y_{2}](x-x_{0})(x-x_{1}) $$

con

$$ [y_{0}]=y_{0},\quad[y_{0},y_{1}]=\frac{y_{1}-y_{0}}{x_{1}-x_{0}}=\frac{y_{1}-y_{0}}{h}, $$$$ [y_{0},y_{1},y_{2}]=\frac{[y_{1},y_{2}]-[y_{0},y_{1}]}{x_{2}-x_{0}}=\frac{1}{2h}\big(\frac{y_{2}-y_{1}}{h}-\frac{y_{1}-y_{0}}{h}\big)=\frac{1}{2h^{2}}\big(y_{0}-2y_{1}+y_{2}\big). $$$$ [y_{0}]=y_{0},\quad[y_{0},y_{1}]=\frac{y_{1}-y_{0}}{h},\quad[y_{0},y_{1},y_{2}]=\frac{1}{2h^{2}}(y_{0}-2y_{1}+y_{2}). $$

Si derivamos $p(x)$

$$ f'(x)\approx p'(x)=[y_{0},y_{1}]+[y_{0},y_{1},y_{2}]((x-x_{0})+(x-x_{1})), $$

Sustituyendo $x$ por $x_0$ obtenemos una fórmula progresiva de orden 2

$$ f'(x_{0})\approx p'(x_{0})=[y_{0},y_{1}]+[y_{0},y_{1},y_{2}]((x_{0}-x_{0})+(x_{0}-x_{1})), $$$$ f'(x_{0})\approx\frac{y_{1}-y_{0}}{h}+\frac{1}{2h^{2}}\big(y_{0}-2y_{1}+y_{2}\big)(-h), $$$$ f'(x_{0})\approx\frac{-3y_{0}+4y_{1}-y_{2}}{2h}. $$

Sustituyendo $x$ por $x_1$, la fórmula centrada que ya teníamos

$$ f'(x_{0})\approx p'(x_{0})=[y_{0},y_{1}]+[y_{0},y_{1},y_{2}]((x_{0}-x_{0})+(x_{0}-x_{1})), $$$$ f'(x_{0})\approx\frac{y_{1}-y_{0}}{h}+\frac{1}{2h^{2}}\big(y_{0}-2y_{1}+y_{2}\big)(-h), $$$$ f'(x_{0})\approx\frac{-3y_{0}+4y_{1}-y_{2}}{2h}. $$

Sustituyendo $x$ por $x_3$ obtenemos una fórmula regresiva de orden 2

$$ f'(x_{2})\approx p'(x_{2})=[y_{0},y_{1}]+[y_{0},y_{1},y_{2}]((x_{2}-x_{0})+(x_{2}-x_{1})), $$$$ f'(x_{2})\approx\frac{y_{1}-y_{0}}{h}+\frac{1}{2h^{2}}\big(y_{0}-2y_{1}+y_{2}\big)(2h+h), $$$$ f'(x_{2})\approx\frac{y_{0}-4y_{1}+3y_{2}}{2h}. $$

Que también podemos escribir de la forma:

$$ \begin{array}{l} \mathbf{Progresiva}\\ f'(\hat x)\approx \frac{1}{2h}(-3f(\hat x)+4f(\hat x+h)-f(\hat x+2h))\\ \mathbf{Centrada}\\ f'(\hat x)\approx \frac{1}{2h}(f(\hat x+h)-f(\hat x-h))\\ \mathbf{Regresiva}\\ f'(\hat x)\approx \frac{1}{2h}(f(\hat x-2h)-4f(\hat x-h)+3f(\hat x)) \end{array} $$

Exercise 2

Dada la función $f(x)=\dfrac{1}{x}$ en $[0.2,1.2]$, y h=0.01.

  • Calcular su derivada aproximada utilizando la fórmula centrada para sus puntos interiores y progresiva y regresiva de orden 1 (dos puntos) para $f'(0.2)$ y $f'(1.2)$ respectivamente.
  • Calcular su derivada aproximada utilizando la fórmula centrada para sus puntos interiores y progresiva y regresiva de orden 2 (tres puntos) para $f'(0.2)$ y $f'(1.2)$ respectivamente.
  • Calcular la derivada exacta en $[0.2,1.2]$ y el error global relativo para las dos aproximaciones.
In [3]:
%run Ejercicio2.py

h            E(df_1)          E(df_2) 

0.010	 1.786397e-02	 2.171714e-03

Derivada segunda de funciones de una variable

A partir del polinomio de interpolación.

$$ p(x)=[y_1]+[y_1,y_2](x-x_1)+[y_1,y_2,y_3](x-x_1)(x-x_2) $$

Derivando dos veces el polinomio anterior obtenemos

$$p''(x_2)=2[y_1,y_2,y_3]= \frac{1}{h^2}(y_1-2y_2+y_3)\quad (1)$$

Ejercicio 3

Dada la función $f(x)=\mathrm{sen}(2\pi x)$ en $[0,1]$ y h=0.01:

Calcular su derivada segunda exacta en $[0,1]$ y su derivada segunda aproximada utilizando la fórmula (1) y el error relativo de la aproximación en el intervalo $[h,1-h]$.

In [4]:
%run Ejercicio3.py

h            Error

0.010	 3.289435e-04

Derivadas de funciones de dos variables

Sea $\Omega =[a,b]\times[c,d]\subset \mathbb{R}^2$. Introducimos particiones uniformes

\begin{eqnarray*} a=x_1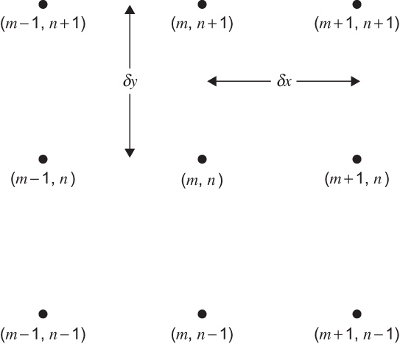Si llamamos a un punto $(x_m,y_n)$ sus vecinos son

Podemos construir las fórmulas de forma análoga a como hicimos con las fórmulas para una variable. Por ejemplo

  • Derivada parcial (progresiva):

$\partial_x f(x_m,y_n)$

$$ (\delta_x^+f)(x_m,y_n)= \frac{f(x_{m+1},y_n)-f(x_{m},y_n)}{h_x} $$
  • Gradiente (centrado):

$\nabla f(x_m,y_n)=(\partial_x f(x_m,y_n),\partial_y f(x_m,y_n))$

$$ \left(\frac{f(x_{m+1},y_n)-f(x_{m-1},y_n)}{2h_x}, \frac{f(x_{m},y_{n+1})-f(x_{m},y_{n-1})}{2h_y}\right)\quad (2) $$
  • Divergencia (centrada):

$\mathrm{div} (\mathbb{f}(x_m,y_n))=\partial_x f_1(x_m,y_n)+\partial_y f_2(x_m,y_n)$

$$ \frac{f_1(x_{m+1},y_n)-f_1(x_{m-1},y_n)}{2h_x}+ \frac{f_2(x_{m},y_{n+1})-f_2(x_{m},y_{n-1})}{2h_y} \quad (3) $$
  • Laplaciana (centrada):

$\Delta f(x_m,y_n)=\partial_{xx} f(x_m,y_n)+ \partial_{yy} f(x_m,y_n)$

$$ \frac{f(x_{m+1},y_n)-2f(x_m,y_n)+f(x_{m-1},y_n)}{h_x^2}+ \frac{f(x_{m},y_{n+1})-2f(x_m,y_n)+f(x_{m},y_{n-1})}{h_y^2} \quad (4) $$

Pero antes de usar estas fórmulas, recordemos como se representan las funciones de dos variables, tanto escalares como vectoriales, en python.

Se representan las funciones de dos variables en coordenadas cartesianas en dominios rectangulares. Como en el caso de las funciones de una variable nosotros decidimos el número de puntos que utilizaremos en la representación.

Carguemos primero las librerías necesarias

In [5]:
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.cm as cm
from mpl_toolkits.mplot3d import Axes3D

Si queremos representar la función escalar $f(x,y)=x^2+y^2$ en $x \in [0,5]$ con paso $h_x=1$ e $y \in [-2,2]$ con paso $h_y=1$, primero creamos la malla

In [6]:
h = 1.
x = np.arange(0., 5. + h, h)
y = np.arange(-2., 2. + h, h)
x, y = np.meshgrid(x, y)

y hemos creado dos matrices

In [7]:
print(x)

[[ 0.  1.  2.  3.  4.  5.]
 [ 0.  1.  2.  3.  4.  5.]
 [ 0.  1.  2.  3.  4.  5.]
 [ 0.  1.  2.  3.  4.  5.]
 [ 0.  1.  2.  3.  4.  5.]]
In [8]:
print(y)

[[-2. -2. -2. -2. -2. -2.]
 [-1. -1. -1. -1. -1. -1.]
 [ 0.  0.  0.  0.  0.  0.]
 [ 1.  1.  1.  1.  1.  1.]
 [ 2.  2.  2.  2.  2.  2.]]

Calculamos ahora los valores de $z=f(x,y)=x^2+y^2$ para cada par de $(x_{ij},y_{ij}) \quad i=1,\ldots,m,\,j=1,\ldots,n$ siendo $m$ y $n$ el número de filas y columnas tanto de x como de y. Operando elemento a elemento obtenemos una matriz z de dimensiones $m\times n$

In [9]:
z = -(x**2 + y**2)
print(z)

[[ -4.  -5.  -8. -13. -20. -29.]
 [ -1.  -2.  -5. -10. -17. -26.]
 [ -0.  -1.  -4.  -9. -16. -25.]
 [ -1.  -2.  -5. -10. -17. -26.]
 [ -4.  -5.  -8. -13. -20. -29.]]

Con estas tres matrices x, y, z ya podemos representar la función $f$.

In [10]:
fig = plt.figure(figsize=(8,6))

ax = fig.add_subplot(221, projection='3d')
ax.plot_surface(x, y, z, rstride=1, cstride=1, linewidth=0,
                cmap=cm.coolwarm)

ax = fig.add_subplot(222, projection='3d')
ax.plot_wireframe(x, y, z)

ax = fig.add_subplot(223)
plt.contour(x, y, z)

ax = fig.add_subplot(224)
plt.contourf(x, y, z)
plt.colorbar();

plt.suptitle(r'$f(x,y)=-x^2-y^2$', fontsize=20);

Si queremos representar una función vectorial $\mathbb{f}=(f_1(x,y),f_2(x,y))$ podemos usar el comando quiver

In [11]:
f1 = lambda x, y: (x**2 + y**2)/3
f2 = lambda x, y: (x**2 - y**2)/2
plt.figure()
ax = plt.gca()
ax.quiver(x,y,f1(x,y),f2(x,y))
ax.set_xlim([-1,6])
ax.set_ylim([-3,3]);

La orden numpy

fy, fx = np.gradient(f,hx,hy)

devuelve el gradiente (calculado numéricamente) de la función escalar f, usando los pasos hx y hy. Lo calcula usando una fórmula centrada de orden dos para los puntos interiores y diferencias de orden uno o dos, progresivas o regresivas en los bordes.

Por lo tanto, la matriz que devuelve tiene las mismas dimensiones que las matrices de los argumentos de entrada.

Exercise 4

Calcular el gradiente de una función usando la orden numpy gradient:

  • Dibujar a función $f(x,y)=x e^{-x^2-y^2}$ en $[-2,2]\times[-2,2]$ con hx=0.1 y hy=0.1.
  • Calcular el gradiente de $f$ y dibujarlo en la misma figura con la función $f$.
  • Calcular el error global relativo de la aproximación usando np.linalg.norm.
In [12]:
%run Ejercicio4.py

Error relativo = 0.012265

Ejercicio 5

  • Calcular la divergencia de $\mathbb{f}(x,y)=(f_1(x,y),f_2(x,y))(x^2+y^2,x^2-y^2)$ en $[-2,2]\times[-2,2]$ utilizando las salidas de la función gradient para las funciones $f_1$ y $f_2$, con hx=0.1 y hy=0.1. Dibujar en la misma figura $\mathbb{f}$ y $\text{div} (\mathbb{f})$
  • Se aprecia un efecto en los bordes debido a una mala aproximación de la divergencia en estos puntos. Rehacer los dibujos restringiendo la representación de la divergencia a $[-2+h_x,2-h_x]\times[-2+h_y,2-h_y]$.
  • Calcular el error global relativo en ambos casos usando np.linalg.norm.
In [13]:
%run Ejercicio5.py

Error relativo 1 = 9.333167e-03
Error relativo 2 = 9.847095e-16

Ejercicio 6

  • Calcular, usando la fórmula (4), la laplaciana de $f(x,y)=x e^{-x^2-y^2}$ en $[-2+h_x,2-h_x]\times[-2+h_y,2-h_y]$ con hx=0.1 y hy=0.1. Dibuja la función y su Laplaciana.
  • Calcular la solución exacta y el error global relativo usando np.linalg.norm.
In [14]:
%run Ejercicio6.py

Error relativo = 5.734265e-03