Integración numérica¶
Fórmulas de cuadratura¶
Las fórmulas de integración numérica o de cuadratura son de la forma:
$$ \int_{a}^{b}f(x)\,dx\approx \omega_{0}\;f(x_{0})+\omega_{1}\;f(x_{1})+\cdots +\omega_{N}\;f(x_{N}) $$donde $x_{0},x_{1},...,x_{N}$ (nodos) son $N+1$ puntos distintos pertenecientes al intervalo $[a,b]$ y $\omega_{0},\omega_{1},\ldots ,\omega_{N}$ (pesos) son números reales.
Fórmulas interpolatorias¶
Si $P_{N}$ es el polinomio que interpola a $f$ en los puntos distintos $x_{0},x_{1},...,x_{N} \in \left[ a,b\right]$ y
$$ \int_{a}^{b}f(x)\,dx\approx \int_{a}^{b}P_N(x)\,dx=\omega_{0}\,f(x_{0})+\omega_{1}\,f(x_{1})+\cdots +\omega_{N}\,f(x_{N}) $$decimos que la fórmula de cuadratura es de tipo interpolatorio.
Fórmulas de cuadratura simples y compuestas¶
Las fórmulas de cuadratura se llaman simples si la aproximación se hace en el intervalo completo $[a,b]$, y compuestas si, antes de aplicar la fórmula, dividimos el intervalo $[a,b]$, en $n$ subintervalos.
Grado de precisión¶
Una fórmula de cuadratura tiene grado de precisión $r$ si es exacta para
$$ f\left( x\right) =1,\quad f\left( x\right) =x,\quad f\left( x\right) =x^{2},...,\quad f\left( x\right) =x^{r}$$pero no es exacta para $f\left( x\right) =x^{r+1}$
Fórmulas de cuadratura de Newton-Cotes simples¶
Son fórmulas de cuadratura de tipo interpolatorio, eligiendo los puntos de interpolación (nodos de la fórmula) igualmente separados de una de las dos formas siguientes:
- Fórmulas cerradas Los límites de integración $a$ y $b$ son nodos de la fórmula.

- Fórmulas abiertas Ninguno de los límites de integración es nodo de la fórmula.
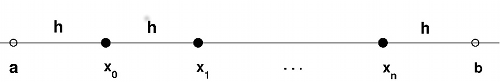
Escribir la función dibujo(f,a,b,nodos) que tiene como argumentos de entrada la función lambda f a integrar, los extremos del intervalo de integración a y b, y los nodos con los que vamos a construir la fórmula interpolatoria en un array numpy nodos y que dibuja
- El área calculada por la integral exacta.
- Los nodos.
- El área aproximada calculada por la fórmula interpolatoria que usa los nodos.
Probar la fórmula con los siguientes datos:
- $f(x) = e^x$, $[a,b]=[0,3]$ y
nodos = np.array([1,2,2.5]) - $f(x) = \cos(x) + 1.5$, $[a,b]=[-3,3]$ y
nodos = np.array([-3.,-1,0,1,3])
Nota
- Si queremos dibujar una poligonal que une tres puntos $(x_0,y_0),$ $(x_1,y_1)$ y $(x_2,y_2)$ con una línea roja discontinua
plt.plot([x0,x1,x2],[y0,y1,y2],'r--')
%run Ejercicio1plot
Calculemos primero una integral de forma exacta (simbólica) para comparar los sucesivos resultados numéricos
Cargamos los paquetes numpy y sympy
import numpy as np
import sympy as sym
La integral
$$ \int_1^3 \ln(x) \,dx \qquad (1) $$se calcula de forma exacta
x = sym.Symbol('x', real=True)
f_sim = sym.log(x)
I_exacta = sym.integrate(f_sim,(x,1,3))
print(I_exacta)
Que también podemos escribir
I_exacta = float(I_exacta)
print(I_exacta)
Fórmula del punto medio¶
La fórmula del punto medio es
$$\int_{a}^{b}f(x)\,dx\approx (b-a)\;f\left( \frac{a+b}{2}\right)$$Usar la fórmula del punto medio para integrar una función en un intervalo, equivale a sustituir, dentro de la integral, la función a integrar por el polinomio de interpolación de grado cero, es decir, una recta horizontal que pasa por el punto de la curva que corresponde al punto medio del intervalo $[a,b]$. Sustituimos la función por una recta e integramos. Estamos entonces calculando el área de un rectángulo.
Escribir la función punto_medio(f,a,b) que tiene como argumentos de entrada la función f a integrar y los extremos del intervalo de integración a y b, y que devuelve el valor aproximado de la integral utilizando la Regla del Punto Medio.
Calcular la integral
$$\int_1^3 \ln(x) \,dx$$Escribir el valor exacto (calculado antes) y el valor aproximado.
%run Ejercicio1a.py
Fórmula de los trapecios¶
La fórmula de los trapecios simple es
$$\int_{a}^{b}f(x)dx\approx \frac{b-a}{2}\;\left( f\left( a\right) +f\left( b\right) \right)$$Usar la fórmula de los trapecios para integrar una función en un intervalo, equivale a sustituir, dentro de la integral, la función a integrar por el polinomio de interpolación de grado uno, que pasa por los puntos de la función de los extremos del intervalo. Es decir, sustituimos la función por una recta e integramos. Estamos entonces calculando el área de un trapecio.
Escribir la función trapecio(f,a,b) del ejemplo anterior que tiene como argumentos de entrada la función $f$ a integrar y los extremos del intervalo de integración $a$ y $b$, y que devuelve el valor aproximado de la integral utilizando la Regla del Trapecio.
Calcular la integral
$$\int_1^3 \ln(x) \,dx$$Escribir el valor exacto y el valor aproximado.
%run Ejercicio1b.py
Fórmula de Simpson¶
La fórmula de Simpson simple es
$$\int_{a}^{b}f(x)dx\approx \frac{b-a}{6}\;\left( f\left( a\right) +4\;f\left( \frac{a+b}{2}\right) +f\left( b\right) \right)$$Usar la fórmula de Simpson para integrar una función en un intervalo, equivale a sustituir, dentro de la integral, la función a integrar por el polinomio de interpolación de grado dos, que pasa por los puntos de la función de los extremos y el punto medio del intervalo. Es decir, sustituimos la función por una parábola e integramos.
Escribir la función simpson(f,a,b) del ejemplo anterior que tiene como argumentos de entrada la función f a integrar y los extremos del intervalo de integración a y b, y que devuelve el valor aproximado de la integral utilizando la Regla del Simpson.
Calcular la integral
$$\int_1^3 \ln(x) \,dx$$Escribir el valor exacto y el valor aproximado.
%run Ejercicio1c.py
Fórmulas de cuadratura de Newton-Cotes compuestas¶
Una forma de disminuir el error de las fórmulas anteriores es aumentar el número de nodos utilizando las fórmulas compuestas. Estas se obtienen dividiendo el intervalo $\left[ a,b\right] $ en $n$ subintervalos y aplicando a cada uno de estos subintervalos una fórmula de cuadratura sencilla.
Si dividimos el intervalo $\left[ a,b\right] $ en $n$ subintervalos de igual longitud usando los nodos $x_{0},x_{1},...,x_{n}$,
la longitud de un subintervalo es
$$h=\frac{b-a}{n}$$los nodos son
$$x_i=a+i\,h \quad i=0,1,\ldots,n$$y el punto medio de un intervalo es
$$\bar x_i =\frac{x_{i-1}+x_i}{2}$$entonces, las fórmulas compuestas se pueden escribir:
Fórmula del punto medio compuesta¶
$$ \int_a^b f dx \approx h\sum_{i=1}^{n}f(\bar x_i)$$Escribir la función punto_medio_comp(f,a,b,n) que tiene como argumentos de entrada la función f a integrar, los extremos del intervalo de integración a y b, y el número de subintervalos que vamos a usar en la fórmula compuesta n y devuelve el valor aproximado utilizando la Regla del Trapecio compuesta.
Calcular, con n = 5 subintervalos, la integral
Escribir el valor exacto y el valor aproximado.
%run Ejercicio1d.py
Regla de los trapecios compuesta¶
$$ \int_a^b f dx \approx \frac{h}{2}(f(a)+f(b))+h\sum_{i=1}^{n-1}f(x_i)$$Escribir la función trapecio_comp(f,a,b,n) que tiene como argumentos de entrada la función f a integrar, los extremos del intervalo de integración a y b y el número de subintervalos que vamos a usar en la fórmula compuesta n y devuelve el valor aproximado utilizando la Regla del Trapecio compuesta.
Calcular, con n = 4 subintervalos, la integral
Escribir el valor exacto y el valor aproximado.
%run Ejercicio1e.py
Fórmula de Simpson Compuesta¶
$$ \int_a^b f dx \approx \frac{h}{6}\sum_{i=1}^{n}\left(f(x_{i-1})+4f(\bar x_i)+f(x_i)\right)) $$Escribir la función simpson_comp(f,a,b,n) que tiene como argumentos de entrada la función f a integrar, los extremos del intervalo de integración a y b y el número de subintervalos que vamos a usar en la fórmula compuesta n y devuelve el valor aproximado utilizando la Regla del Punto Medio compuesta.
Calcular, con n = 4 subintervalos, la integral
Escribir el valor exacto y el valor aproximado.
%run Ejercicio1f.py
Fórmulas de cuadratura gaussianas¶
En la fórmula de cuadratura:
$$ \int_{a}^{b}f(x)dx\approx \omega_{0}f(x_{0})+\omega_{1}f(x_{1})+\cdots +\omega_{N}f(x_{N}) $$¿Es posible calcular los pesos $\omega_i$ y los nodos $x_i$ de forma que la precisión de la fórmula sea lo mayor posible? Sí, pero entonces los nodos no estarán equiespaciados.
Si $[a,b]=[-1,1]$ los pesos y nodos son
Estos nodos y pesos de la fórmula de Gauss-Legendre con nodos se pueden obtener con np.polynomial.legendre.leggauss(n). Por ejemplo, para $n = 1$:
n = 1
[x, w] = np.polynomial.legendre.leggauss(n)
print('w\n',w)
print('x\n',x)
Así, por ejemplo, la fórmula gaussiana para un punto es
$$ \int_{-1}^{1}f(x)\,dx\approx 2\;f(0) $$Para dos puntos
n = 2
[x, w] = np.polynomial.legendre.leggauss(n)
print('w\n',w)
print('x\n',x)
Para tres puntos
n = 3
[x, w] = np.polynomial.legendre.leggauss(n)
print('w\n',w)
print('x\n',x)
Y así sucesivamente.
Estos resultados se pueden generalizar a cualquier intervalo $[a,b]$ cambiando los $x_i$ por $y_i$ de acuerdo con la fórmula
$$y_i=\frac{b-a}{2}x_i+\frac{a+b}{2}$$Y entonces la fórmula de cuadratura es
$$ \int_{a}^{b}f(x)dx\approx\frac{b-a}{2}\left( \omega_{0}\;f(y_{0})+\omega_{1}\;f(y_{1})+\cdots +\omega_{n}\;f(y_{n})\right) $$Escribir la función gauss(f,a,b,n) que tiene como argumentos de entrada la función f a integrar, los extremos del intervalo de integración a y b y el número de nodos n y devuelve el valor aproximado utilizando la fórmulas gaussianas con n = 1, n = 2 y n = 3 nodos la integral
Escribir el valor exacto y el valor aproximado.
%run Ejercicio2.py
Grado de precisión de las fórmulas de cuadratura¶
Grado de precisión¶
Una fórmula de cuadratura tiene grado de precisión $r$ si es exacta para
$$ f\left( x\right) =1,\quad f\left( x\right) =x,\quad f\left( x\right) =x^{2},...,\quad f\left( x\right) =x^{r}$$pero no es exacta para $f\left( x\right) =x^{r+1}$
Escribir una función newton_cotes(f,a,b,n) que devuelva el valor de la integral aproximada de $f$ en el intervalo $[a,b]$ con la función punto_medio si n = 1, trapecio si n = 2 y Simpson si n = 3 donde n es el número de nodos usado en la fórmula.
Escribir la función grado_de_precision(formula,n) que tiene como argumento de entrada la función formula que puede ser la función newton_cotes o gauss y donde n es el número de nodos que se usa en la construcción de la fórmula, que estudia el grado de precisión de cada una de estas fórmulas calculando su error para las integrales
y cuando el error es distinto de cero, para. Imprimir los errores para cada polinomio y el grado de precisión de la fórmula.
Notas:
- Debido a los errores de redondeo, considerar que el error es cero cuando es menor que $10^{-10}$.
%run Ejercicio3.py
Ejercicios propuestos¶
Integración numérica con órdenes python¶
El módulo scipy.integrate provee varias funciones con diferentes técnicas de integración. Entre sus funciones está la función de propósito general quad.
from scipy.integrate import quad
f = lambda x : np.log(x)
a = 1.; b = 3;
I = quad(f,a,b)
print('El valor aproximado es', I[0])
print('El valor exacto es ', I_exacta)
Integración de Montecarlo¶
Podemos calcular integrales aproximadas usando números aleatorios.
Consideremos, de momento, que la función es positiva en el intervalo de integración $[a,b]$. El valor de la integral de la función es igual al área bajo la curva. Para aproximar este área:
- Generamos puntos aleatorios dentro del rectángulo $[a,b]\times[0,\max (f)].$
- Contamos el número de puntos por debajo de la curva.
- La proporción del número de puntos por debajo de la curva relativa a los puntos totales, multiplicada por el área del anterior rectángulo nos da el área aproximada.
Escribir la función montecarlo(f,a,b,n) que tiene como argumentos de entrada la función f a integrar, los extremos del intervalo de integración a y b y el número de puntos aleatorios n y devuelve el valor aproximado utilizando el método de Montecarlo.
Escribir el valor exacto y el valor aproximado.
Nota
Para calcular n puntos aleatorios distribuidos uniformemente en el intervalo $[a,b]$ podemos usar np.random.rand(n) * (b-a) + a.
%run Ejercicio4.py
%run Ejercicio5.py
