Integración numérica
Contenidos
Introducción
Fórmula de cuadratura
Las fórmulas de integración numérica o de cuadratura son de la forma: \[ \int_{a}^{b}f(x)dx\approx \omega_{0}f(x_{0})+\omega_{1}f(x_{1})+\cdots +\omega_{n}f(x_{N}) \] donde \(x_{0},x_{1},...,x_{N}\) (nodos) son \(N+1\) puntos distintos pertenecientes al intervalo \([a,b]\) y \(\omega_{0},\omega_{1},\ldots ,\omega_{N}\) (pesos) son números reales.
Fórmula interpolatoria
Si \(P_{N}\) es el polinomio que interpola a \(f\) en los puntos distintos \(x_{0},x_{1},...,x_{N} \in \left[ a,b\right]\) y \[ \int_{a}^{b}f(x)dx\approx \int_{a}^{b}P_N(x)dx=\omega_{0}f(x_{0})+\omega_{1}f(x_{1})+\cdots +\omega_{n}f(x_{N}) \] decimos que la fórmula de cuadratura es de tipo interpolatorio.
Grado de precisión
Una fórmula de cuadratura tiene grado de precisión \(r\) si es exacta para \[f\left( x\right) =1,\quad f\left( x\right) =x,\quad f\left( x\right) =x^{2},...,f\left( x\right) =x^{r}\] pero no es exacta para \(f\left( x\right) =x^{r+1}\)
Fórmulas de cuadratura de Newton-Cotes simples
Son fórmulas de cuadratura de tipo interpolatorio, eligiendo los puntos de interpolación (nodos de la fórmula) igualmente separados de una de las dos formas siguientes:
- Fórmulas cerradas Los límites de integración \(a\) y \(b\) son nodos de la fórmula.

- Fórmulas abiertas Ninguno de los límites de integración es nodo de la fórmula.

FÓRMULA DEL PUNTO MEDIO
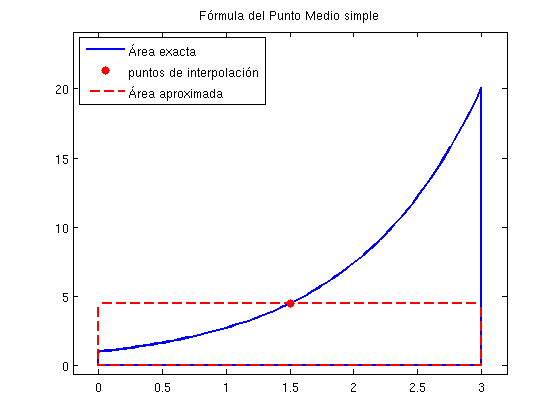
La fórmula del punto medio es \[\int_{a}^{b}f(x)dx\approx (b-a)f\left( \frac{a+b}{2}\right)\] Usar la fórmula del punto medio para integrar una función en un intervalo, equivale a sustituir, dentro de la integral, la función a integrar por el polinomio de interpolación de grado cero, es decir, una recta horizontal que pasa por el punto medio de la función. Sustituimos la función por una recta e integramos. Estamos entonces calculando el área de un rectángulo.
f=@(x) exp(x);a=0;b=3; [valor_aproximado valor_exacto]=punto_medio(f,a,b);
fprintf('El valor exacto es %7.4f\nEl valor aproximado es %7.4f\n',... valor_exacto, valor_aproximado)
El valor exacto es 19.0855 El valor aproximado es 13.4451
Ejercicio 1 Escribir una función llamada punto_medio.m que tiene como argumentos de entrada la función \(f\) a integrar y los extremos del intervalo de integración \(a\) y \(b\) que devuelve el valor aproximado utilizando la Regla del Punto Medio y el valor exacto.
Ejercicio 2 Integrando polinomios de distinto grado, decidir cual es el grado de precisión de la Fórmula del Punto Medio.
FÓRMULA DE LOS TRAPECIOS
La fórmula de los trapecios simple es \[\int_{a}^{b}f(x)dx\approx \frac{b-a}{2}\left( f\left( a\right) +f\left( b\right) \right)\] Usar la fórmula de los trapecios para integrar una función en un intervalo, equivale a sustituir, dentro de la integral, la función a integrar por el polinomio de interpolación de grado uno, que pasa por los puntos de la función de los extremos del intervalo. Es decir, sustituimos la función por una recta e integramos. Estamos entonces calculando el área de un trapecio.
f=@(x) exp(x);a=0;b=3; [valor_aproximado valor_exacto]=trapecio(f,a,b);

fprintf('El valor exacto es %7.4f\nEl valor aproximado es %7.4f\n',... valor_exacto, valor_aproximado)
El valor exacto es 19.0855 El valor aproximado es 31.6283
Ejercicio 3 Escribir una función llamada trapecio.m que tiene como argumentos de entrada la función \(f\) a integrar y los extremos del intervalo de integración \(a\) y \(b\) que devuelve el valor aproximado utilizando la Regla del Trapecio y el valor exacto.
Ejercicio 4 Integrando polinomios de distinto grado, decidir cual es el grado de precisión de la Fórmula de los Trapecios.
FÓRMULA DE SIMPSON
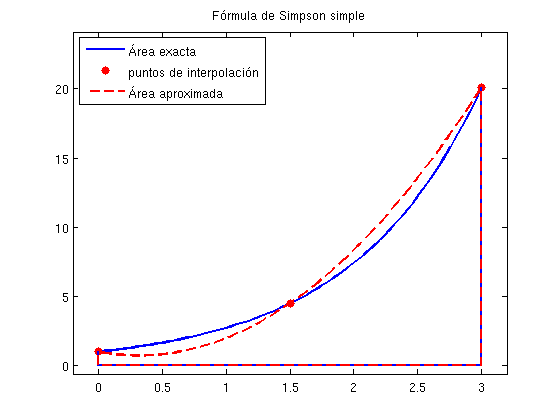
La fórmula de Simpson simple es \[\int_{a}^{b}f(x)dx\approx \frac{b-a}{6}\left( f\left( a\right) +4f\left( \frac{a+b}{2}\right) +f\left( b\right) \right)\] Usar la fórmula de Simpson para integrar una función en un intervalo, equivale a sustituir, dentro de la integral, la función a integrar por el polinomio de interpolación de grado dos, que pasa por los puntos de la función de los extremos y el punto medio del intervalo. Es decir, sustituimos la función por una parábola e integramos.
f=@(x) exp(x);a=0;b=3; [valor_aproximado valor_exacto]=simpson(f,a,b);
fprintf('El valor exacto es %7.4f\nEl valor aproximado es %7.4f\n',... valor_exacto, valor_aproximado)
El valor exacto es 19.0855 El valor aproximado es 19.5061
Ejercicio 4 Escribir una función llamada simpson.m que tiene como argumentos de entrada la función \(f\) a integrar y los extremos del intervalo de integración \(a\) y \(b\) que devuelve el valor aproximado utilizando la Regla de Simpson y el valor exacto.
Ejercicio 5 Integrando polinomios de distinto grado, decidir cual es el grado de precisión de la Fórmula de Simpson.
Fórmulas de cuadratura de Newton-Cotes compuestas
Aunque vemos que, en general, la fórmula de Simpson proporciona un error menor que la regla de los trapecios, y esta a su vez proporciona un error menor que la regla del punto medio, al aumentar el número de nodos de las fórmulas simples, el error no tiende a cero. Una alternativa para disminuir el error es aumentar el número de nodos utilizando las fórmulas compuestas. Estas se obtienen dividiendo el intervalo \(\left[ a,b\right] \) en \(n\) subintervalos y aplicando a cada uno de estos subintervalos una fórmula de cuadratura sencilla.
Sea \[\bar x_n =\frac{x_{n-1}+x_n}{2}\]
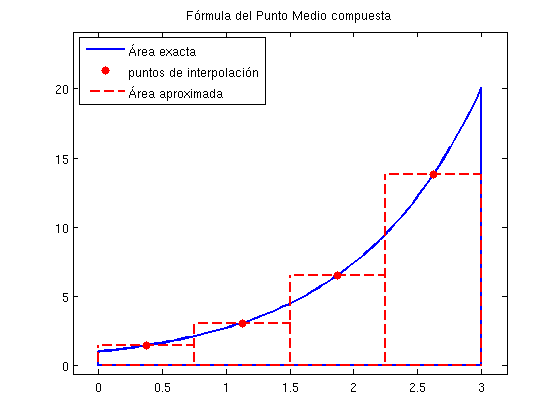
FÓRMULA DEL PUNTO MEDIO COMPUESTA
\[ \int_a^b f dx \approx h\sum_{n=1}^{N}f(\bar x_n)\]
f=@(x) exp(x);a=0;b=3;N=4; [valor_aproximado valor_exacto]=punto_medio_comp(f,a,b,N);
fprintf('El valor exacto es %7.4f\nEl valor aproximado es %7.4f\n',... valor_exacto, valor_aproximado)
El valor exacto es 19.0855 El valor aproximado es 18.6455
Ejercicio 7
- Escribir una función llamada punto_medio_comp.m que tiene como argumentos de entrada la función \(f\) a integrar, los extremos del intervalo de integración \(a\) y \(b\) y el número de subintervalos que vamos a usar en la fórmula compuesta \(N\) y devuelve el valor aproximado utilizando la Regla del Punto Medio compuesta y el valor exacto.
- Hacer una tabla con los errores obtenidos al integrar \[\int_{0}^{\pi} \sin(x)dx\] utilizando \(N=4,8,16,32\) subintervalos.
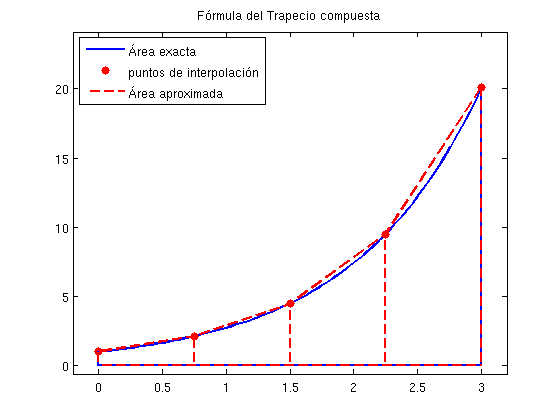
REGLA DE LOS TRAPECIOS COMPUESTA \[ \int_a^b f dx \approx \frac{h}{2}(f(a)+f(b))+h\sum_{n=1}^{N-1}f(x_n)\]
f=@(x) exp(x);a=0;b=3;N=4; [valor_aproximado valor_exacto]=trapecio_comp(f,a,b,N);
fprintf('El valor exacto es %7.4f\nEl valor aproximado es %7.4f\n',... valor_exacto, valor_aproximado)
El valor exacto es 19.0855 El valor aproximado es 19.9719
Ejercicio 8
- Escribir una función llamada trapecio_comp.m que tiene como argumentos de entrada la función \(f\) a integrar, los extremos del intervalo de integración \(a\) y \(b\) y el número de subintervalos que vamos a usar en la fórmula compuesta \(N\) y devuelve el valor aproximado utilizando la Regla del Trapecio compuesta y el valor exacto.
- Hacer una tabla con los errores obtenidos al integrar \[\int_{0}^{\pi} \sin(x)dx\] utilizando \(N=4,8,16,32\) subintervalos.
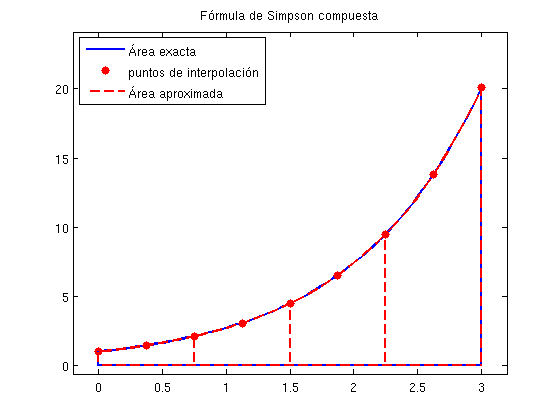
FÓRMULA DE SIMPSON COMPUESTA \[ \int_a^b f dx \approx \frac{h}{6}\sum_{n=1}^{N}\left(f(x_{n-1})+4f(\bar x_n)+f(x_n)\right)) \]
f=@(x) exp(x);a=0;b=3;N=4; [valor_aproximado valor_exacto]=simpson_comp(f,a,b,N);
fprintf('El valor exacto es %7.4f\nEl valor aproximado es %7.4f\n',... valor_exacto, valor_aproximado)
El valor exacto es 19.0855 El valor aproximado es 19.0876
Ejercicio 9
- Escribir una función llamada simpson_comp.m que tiene como argumentos de entrada la función \(f\) a integrar, los extremos del intervalo de integración \(a\) y \(b\) y el número de subintervalos que vamos a usar en la fórmula compuesta \(N\) y devuelve el valor aproximado utilizando la Regla del Punto Medio compuesta y el valor exacto.
- Hacer una tabla con los errores obtenidos al integrar \[\int_0^{\pi} \sin(x)dx\] utilizando \(N=4,8,16,32\) subintervalos.
Fórmulas de cuadratura gaussianas
En la fórmula de cuadratura: \[ \int_{a}^{b}f(x)dx\approx \omega_{0}f(x_{0})+\omega_{1}f(x_{1})+\cdots +\omega_{N}f(x_{N}) \] ¿Es posible calcular los pesos \(\omega_i\) y los nodos \(x_i\) de forma que la precisión de la fórmula sea lo mayor posible? Sí, pero entonces los nodos no estarán equiespaciados.
Si \([a,b]=[-1,1]\) los pesos y nodos son
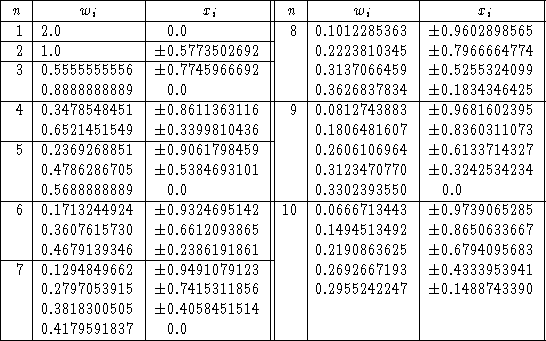
Así, por ejemplo, la fórmula gaussiana para un punto es \[ \int_{-1}^{1}f(x)dx\approx 2 f(0) \] Para dos puntos \[ \int_{-1}^{1}f(x)dx\approx f(-0.5773502692)+f(0.5773502692) \] Para tres puntos \[ \int_{-1}^{1}f(x)dx\approx 0.555555556 f(-0.774596692)+0.8888888889f(0)+ 0.555555556 f(0.774596692) \] Y así sucesivamente.
Estos resultados se pueden generalizar a cualquier intervalo \([a,b]\) cambiando los \(x_i\) por \(y_i\) de acuerdo con la fórmula \[y_i=\frac{b-a}{2}x_i+\frac{a+b}{2}\] Y entonces la fórmula de cuadratura es \[ \int_{a}^{b}f(x)dx\approx\frac{b-a}{2}\left( \omega_{0}f(y_{0})+\omega_{1}f(y_{1})+\cdots +\omega_{n}f(y_{n})\right) \]
Ejercicio 10 Escribir una función llamada gauss.m que tiene como argumentos de entrada la función \(f\) a integrar, los extremos del intervalo de integración \(a\) y \(b\) y el número de puntos de interpolación \(n\) (que podrá ser igual a uno, dos o tres) y devuelve el valor aproximado de la integral utilizando la fórmula gaussiana correspondiente y que devuelve también el valor exacto.
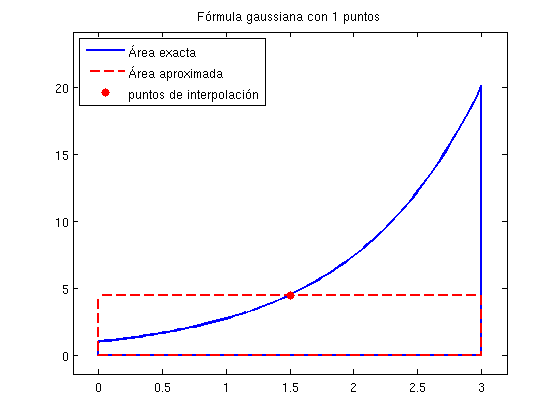
f=@(x) exp(x);a=0;b=3;n=1; [valor_aproximado valor_exacto]=gauss(f,a,b,n);
fprintf('El valor exacto es %7.4f\nEl valor aproximado es %7.4f\n',... valor_exacto, valor_aproximado)
El valor exacto es 19.0855 El valor aproximado es 13.4451
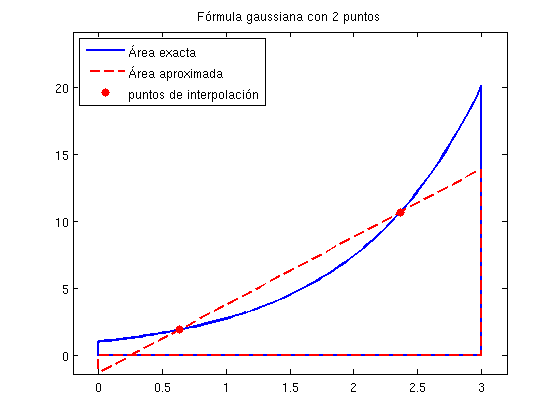
f=@(x) exp(x);a=0;b=3;n=2; [valor_aproximado valor_exacto]=gauss(f,a,b,n);
fprintf('El valor exacto es %7.4f\nEl valor aproximado es %7.4f\n',... valor_exacto, valor_aproximado)
El valor exacto es 19.0855 El valor aproximado es 18.8101
f=@(x) exp(x);a=0;b=3;n=3; [valor_aproximado valor_exacto]=gauss(f,a,b,n);
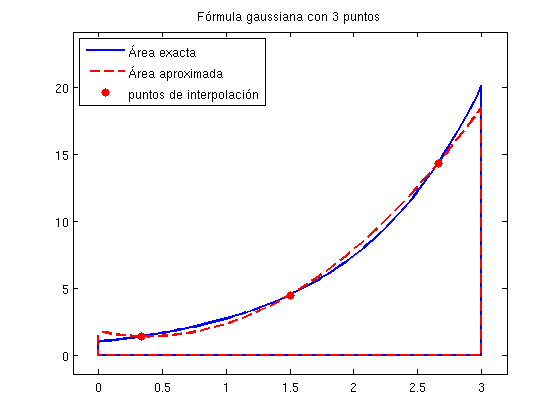
fprintf('El valor exacto es %7.4f\nEl valor aproximado es %7.4f\n',... valor_exacto, valor_aproximado)
El valor exacto es 19.0855 El valor aproximado es 19.0803
Ejercicio 11 Comparar cada fórmula de Gauss con la fórmula simple de Newton-Cotes que utiliza el mismo número de puntos de interpolación:
- ¿Para cual de las dos es el error mayor?
- ¿Cual tiene un grado de precisión mayor? Especificar el grado de precisión de cada fórmula.
Integración numérica con órdenes Matlab
Hay varias órdenes que utilizan diferentes métodos. Cada una es adecuada para distintos tipos de funciones. Por ejemplo
- quad puede ser más eficiente para precisiones bajas con integrandos que varíen mucho.
- quadl funciona mejor que quad con precisiones altas e integrandos sin variaciones abruptas.
- quadgk funciona mejor con precisiones altas e integrandos oscilatorios.
- quadv vectoriza quad para integrandos vectoriales.