Resolución de sistemas lineales

Contenidos

Introducción
Métodos iterativos
Métodos directos
La operación \

Introducción

Queremos resolver sistemas de ecuaciones lineales con el mismo número de ecuaciones que de incógnitas con matriz de coeficientes no singular.

Dados los números \(a_{ij}\) y \(b_{j}\) para \(i,j=1,2,\ldots,n\) se trata de hallar los números \(x_{1},x_{2},\ldots,x_{n}\) que verifican las \(n\) ecuaciones lineales \[ \begin{array}{cll} a_{11}x_{1}+a_{12}x_{2}+\ldots+a_{1n}x_{n} & = & b_{1}\\ a_{21}x_{1}+a_{22}x_{2}+\ldots+a_{2n}x_{n} & = & b_{2}\\ \vdots\\ a_{n1}x_{1}+a_{n2}x_{2}+\ldots+a_{nn}x_{n} & = & b_{n} \end{array} \]

Métodos iterativos

Los métodos iterativos son, en general, más eficientes que los métodos directos para resolver sistemas de ecuaciones lineales grandes y con matrices de coeficientes con pocos elementos distintos de cero.

Los métodos iterativos se basan en reescribir el problema \[ A\mathbf{x}=\mathbf{b}\Longleftrightarrow\mathbf{x}=B\mathbf{x}+\mathbf{c} \] donde \(B\) es una matriz \(n\times n\) y \(c\) es un vector columna de dimensión \(n\)

Entonces, si \(\mathbf{x}^{(0)}\) es una aproximación inicial a la solución, para \(k=1,2,\ldots\) \[ \mathbf{x}^{(k)}=B\mathbf{x}^{(k-1)}+\mathbf{c} \]

JACOBI

Algoritmo de Jacobi

Elegir una aproximación inicial \(\mathbf{x}^{(0)}\)
Para \(k=1,2,\ldots,MaxIter\)
----Para \(i=1,2,\ldots,n\) calcular \[ x_{i}^{(k)}=\frac{1}{a_{ii}}(b_{i}-\sum_{j=1}^{i-1}a_{ij}x_{j}^{(k-1)}-\sum_{j=i+1}^{n}a_{ij}x_{j}^{(k-1)}) \]
----Si se cumple el criterio de parada, tomar \(\mathbf{x}^{(k)}\) como aproximación a la solución.

Ejercicio 1. Crear una función [x,n]=jacobi(A,b,tol) que solucione el sistema lineal \(Ax=b\) por el método de Jacobi. \(x\) es la solución del sistema y \(n\) el número de iteraciones realizadas.

Resolver el sistema \[ \begin{cases} 5x_{1}+x_{2}-x_{3}-x_{4} & =1\\ x_{1}+4x_{2}-x_{3}+x_{4} & =1\\ x_{1}+x_{2}-5x_{3}-x_{4} & =1\\ x_{1}+x_{2}+x_{3}-4x_{4} & =1 \end{cases} \] por el método de Jacobi, con tolerancia absoluta \(10^{-4}\). Usar la norma infinito \[ \lvert\lvert\mathrm{x}^{\left(k\right)}-\mathrm{x}^{\left(k-1\right)}\rvert\rvert_{\infty}=\underset{1\leq i\leq n}{\max}\left(\left|x_{i}^{(k)}-x_{i}^{(k-1)}\right|\right) \]

A=[ 5 1 -1 -1; 1 4 -1 1 ; 1 1 -5 -1; 1 1 1 -4];
b=[1;1;1;1];
tol=1e-4;
[x,n]=jacobi(A,b,tol)

Resolver también el sistema \(A_1x=b_1\)

m=30;
A1=magic(m);
for i=1:m,A1(i,i)=norm(A1,inf);end
b1=A1*(m:-1:1)';
tol=1e-4;
[x,n]=jacobi(A1,b1,tol);
sol=x'
iteraciones=n

sol =
  Columns 1 through 7
   30.0000   29.0000   28.0000   27.0000   26.0000   25.0000   24.0000
  Columns 8 through 14
   23.0000   22.0000   21.0000   20.0000   19.0000   18.0000   17.0000
  Columns 15 through 21
   16.0000   15.0000   14.0000   13.0000   12.0000   11.0000   10.0000
  Columns 22 through 28
    9.0000    8.0000    7.0000    6.0000    5.0000    4.0000    3.0000
  Columns 29 through 30
    2.0000    1.0000
iteraciones =
     9

GAUSS-SEIDEL

Algoritmo de Gauss-Seidel

Elegir una aproximación inicial \(\mathbf{x}^{(0)}\)
Para \(k=1,2,\ldots,MaxIter\)
----Para \(i=1,2,\ldots,n\) calcular \[ x_{i}^{(k)}=\frac{1}{a_{ii}}(b_{i}-\sum_{j=1}^{i-1}a_{ij}x_{j}^{(k)}-\sum_{j=i+1}^{n}a_{ij}x_{j}^{(k-1)}) \]
----Si se cumple el criterio de parada, tomar \(\mathbf{x}^{(k)}\) como aproximación a la solución.

Ejercicio 2. Crear una función [x,n]=gauss_seidel(A,b,tol) que solucione el sistema lineal \(Ax=b\) por el método de Gauss-Seidel. Resolver el sistema anterior

[x,n]=gauss_seidel(A,b,tol)

Resolver también el sistema \(A_1x=b_1\)

m=30;
A1=magic(m);
for i=1:m,A1(i,i)=norm(A1,inf);end
b1=A1*(m:-1:1)';
tol=1e-4;
[x,n]=gauss_seidel(A1,b1,tol);
sol=x'
iteraciones=n

sol =
  Columns 1 through 7
   30.0000   29.0000   28.0000   27.0000   26.0000   25.0000   24.0000
  Columns 8 through 14
   23.0000   22.0000   21.0000   20.0000   19.0000   18.0000   17.0000
  Columns 15 through 21
   16.0000   15.0000   14.0000   13.0000   12.0000   11.0000   10.0000
  Columns 22 through 28
    9.0000    8.0000    7.0000    6.0000    5.0000    4.0000    3.0000
  Columns 29 through 30
    2.0000    1.0000
iteraciones =
     5

Ejercicio 3. Modificar las funciones anteriores y llamarlas jacobi2 y gauss_seidel2, de forma que devuelvan la sucesión de soluciones y la sucesión de errores relativos. Utilizarlas para:

Dibujar la sucesión de errores relativos en escala logarímica (usar semilogy en lugar de plot) al resolver el sistema anterior por Jacobi y Gauss-Seidel para una tolerancia relativa \(10^{-6}\).

Ejercicio3a

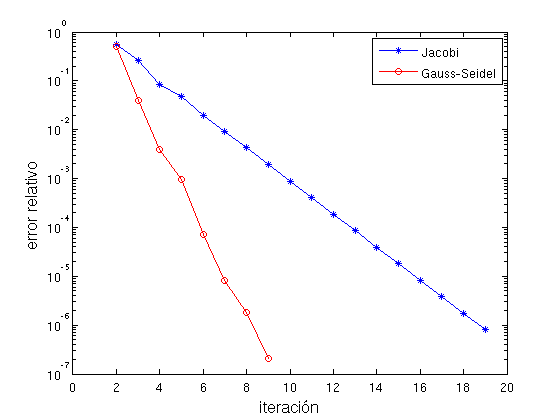
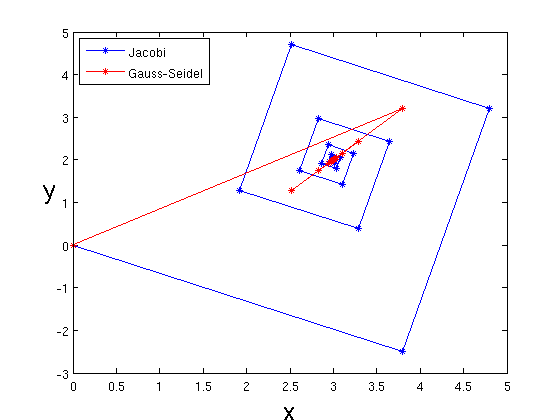
Resolver por Jacobi y Gauss-Seidel el sistema \[ \begin{cases} 5x+2y & =19\\ 3x-2y & =5 \end{cases} \] con tolerancia relativa \(10^{-2}\) y dibujar las sucesivas soluciones en el plano XY.

Ejercicio3b

Métodos directos

FACTORIZACIÓN LU

Descomponemos la matriz de coeficientes \(A\) en una matriz triangular superior \(U\) y una matriz triangular inferior \(L\) de forma que \[ A=LU \] Consideramos el sistema de ecuaciones lineales \[ A\mathbf{x}=\mathbf{b} \] donde la matriz \(A\) admite la factorización \(LU\). Entonces \[ A\mathbf{x}=\mathbf{b}\Longleftrightarrow LU\mathbf{x}=\mathbf{b} \] Factorizaremos la matriz \(A\) usando la orden de Matlab lu

A=[2 1 1;1 2 -1;-1 1 2];
[L U P]=lu(A)

L =
    1.0000         0         0
    0.5000    1.0000         0
   -0.5000    1.0000    1.0000
U =
    2.0000    1.0000    1.0000
         0    1.5000   -1.5000
         0         0    4.0000
P =
     1     0     0
     0     1     0
     0     0     1

Si la función lu reordena las filas se verifica que \(PA=LU\) y estaremos resolviendo \(PAx=Pb\) que es equivalente al sistema \(Ax=b\).

Para resolver el sistema

resolvemos \(L\mathbf{y}=P\mathbf{b}\) usando sustitución progresiva y obtenemos \(\mathbf{y}\).
resolvemos \(U\mathbf{x}=\mathbf{y}\) usando sustitución regresiva y obtenemos \(\mathbf{x}\).

ALGORITMO DE SUSTITUCIÓN PROGRESIVA

Si tenemos un sistema \[ L\mathbf{x}=\mathbf{b} \] donde \(L\) es una matriz triangular inferior:

\[ L=\left(\begin{array}{ccccc} l_{11} & 0 & 0 & \ldots & 0\\ l_{21} & l_{22} & 0 & \ldots & 0\\ l_{31} & l_{32} & l_{33} & \ldots & 0\\ \vdots & \vdots & \vdots & \ddots & \vdots\\ l_{n1} & l_{n2} & l_{n3} & \ldots & l_{nn} \end{array}\right) \] La ecuación \(i\)-ésima del sistema, para \(i=1,2,\ldots,n\) es: \[ l_{i1}x_{1}+l_{i2}x_{2}+\cdots+l_{ii}x_{i}=b_{i} \]

Por lo tanto, para \(i=1,2,\ldots,n\), si \(l_{ii}\) no es \(0\) entonces \[ x_{i}=\frac{b_{i}-l_{i1}x_{1}-\cdots-l_{ii-1}x_{i-1}}{l_{ii}}=\frac{1}{l_{ii}}\left(b_{i}-\sum_{j=1}^{i-1}l_{ij}x_{j}\right) \]

Algoritmo

Si \(l_{11}=0\), parar (no existe solución única).
Hacer \(x_{1}=\frac{b_{1}}{l_{11}}\)
Para \(i=2,\ldots,n\)
-----Si \(l_{ii}=0\), parar (no tiene solución)
-----Hacer \[ x_{i}=\frac{1}{l_{ii}}\left(b_{i}-\sum_{j=1}^{i-1}l_{ij}x_{j}\right) \]

Ejercicio 4. Construir una función x=sust_pro(L,b) donde x es la solución del sistema Lx=b siendo L es una matriz triangular inferior. Resolver el sistema \[\left(\begin{array}{rrr} 2 & 0 & 0\\ 1 & 2 & 0\\ 1 & 1 & 2 \end{array}\right) \left(\begin{array}{c} x_1\\ x_2\\ x_3 \end{array}\right)= \left(\begin{array}{r} 2\\ -1\\ 0 \end{array}\right) \]

L=[2 0 0;1 2 0;1 1 2];
b=[2 -1 0];
x=sust_pro(L,b')

ALGORITMO DE SUSTITUCIÓN REGRESIVA

Si tenemos un sistema \[ U\mathbf{x}=\mathbf{b}' \] donde \(U\) es una matriz triangular superior: \[ U=\left(\begin{array}{ccccc} u_{11} & u_{12} & u_{13} & \ldots & u_{1n}\\ 0 & u_{22} & u_{23} & \ldots & u_{2n}\\ 0 & 0 & u_{33} & \ldots & u_{3n}\\ \vdots & \vdots & \vdots & \ddots & \vdots\\ 0 & 0 & 0 & 0 & u_{nn} \end{array}\right) \] La ecuación \(i\)-ésima del sistema, para \(i=1,2,\ldots,n\) es: \[ u_{ii}x_{i}+u_{ii+1}x_{i+1}+\cdots+u_{in}x_{n}=b_{i} \] Por lo tanto, para \(i=n,n-1,\ldots,1\), si \(u_{ii}\) no es \(0\) entonces \[ x_{i}=\frac{b_{i}-u_{ii+1}x_{i+1}-\cdots-u_{in}x_{n}}{u_{ii}}=\frac{1}{u_{ii}}\left(b_{i}-\sum_{j=i+1}^{n}u_{ij}x_{j}\right) \]

Algoritmo

Si \(u_{nn}=0\), parar (no existe solución única).
Hacer \(x_{n}=\frac{b_{n}}{u_{nn}}\)
Para \(i=n-1,\ldots,1\)
---- Si \(u_{ii}=0\), parar (no tiene solución)
---- Hacer \[ x_{i}=\frac{1}{u_{ii}}\left(b_{i}-\sum_{j=i+1}^{n}u_{ij}x_{j}\right) \]

Ejercicio 5. Construir una función x=sust_re(U,b) donde x es la solución del sistema Ux=b siendo U es una matriz triangular superior. Resolver el sistema \[\left(\begin{array}{rrr} 2 & 1 & 1\\ 0 & 2 & 1\\ 0 & 0 & 2 \end{array}\right) \left(\begin{array}{c} x_1\\ x_2\\ x_3 \end{array}\right)= \left(\begin{array}{r} 9\\ 4\\ 4 \end{array}\right) \]

U=[2 1 1;0 2 1;0 0 2];
b=[9 4 4];
x=sust_re(U,b')

Ejercicio 6. Dado el sistema \(Ax=b\) con \[ A=\left(\begin{array}{rrr} 2 & 1 & 1\\ 1 & 2 & 2\\ 1 & 1 & 2 \end{array}\right)\quad b=\left(\begin{array}{c} 2\\ 4\\ 6 \end{array}\right) \] Resolverlo utilizando la descomposición LU.

Ejercicio6

L =
    1.0000         0         0
    0.5000    1.0000         0
    0.5000    0.3333    1.0000
U =
    2.0000    1.0000    1.0000
         0    1.5000    1.5000
         0         0    1.0000
P =
     1     0     0
     0     1     0
     0     0     1
b1 =
     2
     4
     6
y =
     2
     3
     4
x =
     0
    -2
     4

La operación \

Ejercicio

Resolver el sistema \(Ax=b) utilizando el operador \.

A=[ 5 1 -1 -1; 1 4 -1 1 ; 1 1 -5 -1; 1 1 1 -4];
b=[1;1;1;1];
x=A\b