Introducción a Matlab

Conceptos básicos de programación en Matlab

Contenidos

Ficheros .m
Funciones en ficheros .m
Funciones en línea
Bucles
Condicionales
Referencias

Ficheros .m

Un fichero de código .m es un fichero externo que contiene una secuencia de órdenes en Matlab.

Los ficheros de código usan la extensión .m

Los ficheros .m pueden contener código que consiste en una serie de órdenes Matlab o puede contener funciones que aceptan argumentos que producen uno o más argumentos de salida.

Aquí tenemos dos scripts sencillos:

Ejemplo 1.1 Encontrar la solución del siguiente sistema de ecuaciones:

\[x+2y+3z=1,\quad 3x+3y+4z=1,\quad 2x+3y+3z=2.\]

Solución: escribimos el fichero ejemplo1.m que contiene las siguientes órdenes y ejecutamos.

>> ejemplo1

clear all
A=[1 2 3; 3 3 4; 2 3 3];
b= [1;1;2];
x=A\b

Cuando se ha completado la ejecución, las variables (\(A\), \(b\), \(x\)) permanecen en el "workspace". Para obtener una lista de las variables, introducimos whos en línea de comandos.

whos

  Name      Size            Bytes  Class     Attributes

  A         3x3                72  double              
  b         3x1                24  double              
  x         3x1                24  double

Ejemplo 1.2 Dibujar las siguientes funciones cosenoidales: \(y_1 = 2 \cos(x)\), \(y_2 = \cos(x)\), y \(y_3 = 0.5 \cos(x)\), en el intervalo \([0,2\pi]\). Escribir los comandos en el fichero ejemplo2.m

x = 0:pi/100:2*pi;
y1 = 2*cos(x);
y2 = cos(x);
y3 = 0.5*cos(x);
plot(x,y1,'--',x,y2,'-',x,y3,':')
xlabel(' x ')
ylabel('Funciones cosenoidales')
legend('2*cos(x)','cos(x)','0.5*cos(x)')
title('Ejemplo típico de plot múltiple')
axis([0 2*pi -3 3])

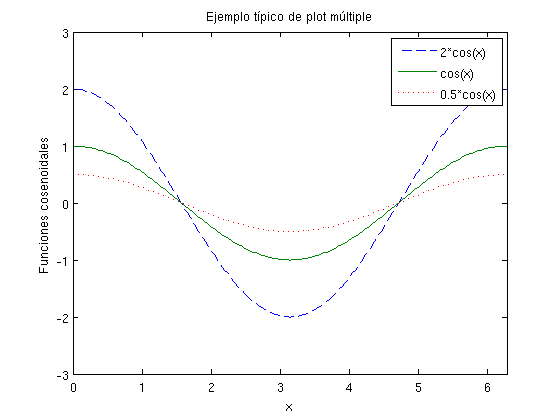
Ejercicio 1.1 Escribir un programa (ejercicio1_1.m) que encuentre las raíces de la ecuación de segundo orden \(ax^2 +bx +c=0\), para cualquier \(a\), \(b\) y \(c\), definiéndolos como \(a=1\), \(b=2\), \(c=3\).

ejercicio1_1

r1 =
  -1.0000 + 1.4142i
r2 =
  -1.0000 - 1.4142i

Funciones en ficheros .m

Las funciones son programas (o rutinas) que aceptan argumentos de entrada y devuelven argumentos de salida.

Cada función .m tiene su propio espacio en el "workspace", separado del "workspace" básico del MATLAB.

El nombre del fichero debe coincidir con el nombre de la función.

La primera línea de una función .m empieza con la palabra function. Nos da el nombre de la función y el nombre y orden de los argumentos.

En estas funciones sencillas se muestran los elementos básicos. Omite % en tu código.

Ejemplo 1.3 función f.m, que evalua el cuadrado de un número.

(Quitar los "%" al escribir lo siguiente en el fichero f.m)

%function z=f(x)
%z=x^ 2;

f(2)

ans =
     4

Ejemplo 1.4 Función measures_sphere.m, que calcula el área y el volumen de una esfera de radio \(R\).

(Quitar los "%" al escribir lo siguiente en el fichero measures_sphere.m)

%function [area,volume]=measures_sphere(R)
%area=4*pi*R.^ 2;
%volume=(4/3)*pi*R.^3;

R=[0:0.1:0.5];
[a,v]=measures_sphere(R)

a =
         0    0.1257    0.5027    1.1310    2.0106    3.1416
v =
         0    0.0042    0.0335    0.1131    0.2681    0.5236

Ejercicio 1.2 Escribe una función (llamada raices) que calcule las raíces de la ecuación del Ejercicio 1.1, pero ahora, con \(a\), \(b\), \(c\) pasados como argumentos.

a=1;b=2;c=3;
[r1 r2]=raices(a,b,c)

r1 =
  -1.0000 + 1.4142i
r2 =
  -1.0000 - 1.4142i

Funciones en línea

También podemos definir funciones sencillas dentro sin usar ficheros .m usando

f=@(x) expresión de la función;

Por ejemplo

Area=@(R) 4*pi*R.^ 2;
Area(R)

ans =
         0    0.1257    0.5027    1.1310    2.0106    3.1416

Ejercicio 1.3 Escribir una función en línea (ejercicio1_3.m) que calcule el volumen de una esfera. Usarla para calcular el volumen de una esfera de radio \(R=0.5\).

ejercicio1_3

ans =
    0.5236

Bucles

Los bucles en Matlab tienen la sintaxis:

%for i=vector
%   conjunto de instrucciones
%end

donde el vector se da, habitualmente, como

          vector = primero:incremento:último

vector1=4:2:17
vector2=7:-1:2

vector1 =
     4     6     8    10    12    14    16
vector2 =
     7     6     5     4     3     2

Si incremento=1, se escribe

          vector = primero:último

vector3=4:10

vector3 =
     4     5     6     7     8     9    10

Ejemplo 1.5 Calcular \(\sum_{k=1}^{5} {k}\) y \(5!\).

Sum=0;Factorial=1;
for k=1:5
  Sum=Sum+k;
  Factorial=Factorial*k;
end
[Sum,Factorial]

ans =
    15   120

Ejercicio 1.4 Escribir un programa que calcule \[\sum_{k=1}^{10}\frac{1}{k^2},\; \prod_{k=1}^{10}\frac{1}{k^2}\].

ejercicio1_4

suma =
    1.5498
producto =
   7.5941e-14

Ejemplo 1.6 Un ejemplo de partición uniforme de \((0,1)\) sería \[(0,0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1)\] Es decir, un vector, con extremos \(0\) y \(1\) y en medio, puntos equiespaciados, en este caso con distancia entre ellos \(dt=0.1\). Hay dos formas de definir una partición uniforme:

Podemos usar la llamada "vectorización".
Podemos usar un bucle for.

La primera forma es más eficiente.

En Matlab, la vectorización a menudo ahorra tiempo de ejecución. La orden tic-toc mide el tiempo de ejecución.

dt=0.001;
% Definimos la malla usando vectorización
tic
t=0:dt:1;
toc
% Definimos la malla usando un bucle
tic
T(1)=0;
for k=2:length(t)
  T(k)=(k-1)*dt;
end
toc
% Discrepancia entre las mallas t y T
disp(['norm(t-T) = ', num2str(norm(t-T))]) % norm(y) -> Norma euclídea de y
                                           % norm(y) = sqrt(sum(y_i^2))
disp(['machine epsilon = ', num2str(eps)])

Elapsed time is 0.000081 seconds.
Elapsed time is 0.002861 seconds.
norm(t-T) = 1.1749e-15
machine epsilon = 2.2204e-16

Observar que norm(t-T) nos debería dar que t==T (en el sentido de la representación en punto flotante).

Pero esto no se cumple debido a la acumulación de errores de redondeo.

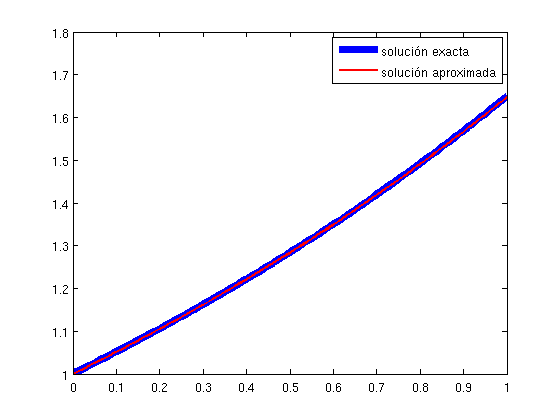
Ejercicio 1.5 La solución exacta de la ecuación diferencial \(f'(t)= f(t)/2\) con la condición inicial \(f(0)=1\) es la función \(f_{exacta}(t)=\exp(t/2)\).

Utilizando un Método Numérico vamos a calcular una solución aproximada. Esta solución consistirá en una serie de puntos que almacenaremos en un vector \(fvector\) y que contendrá los valores de la función aproximada para los puntos de la malla uniforme en \((0,1)\).

Sabemos que \(f_{exacta}(t_0)=1\), por lo tanto \(f_{aprox}(t_0)=1\) y en la primera posición del vector almacenamos fvector(1)=1.

Los demás puntos los calculamos utilizando la fórmula \[ fvector(k+1)=fvector(k)+dt*fvector(k)/2\]

Sigue los pasos:

Define una partición del intervalo \((0,1)\) con dt=0.01.
Inicializa fvector.
Haz un bucle que calcule fvector(k+1)=fvector(k)+dt*fvector(k)/2.
Define f_exacta como una función en línea.
Crea un vector fv_exacta con los valores de f_exacta en los puntos \(t_i\) de la malla.
Calcula el error relativo entre fvector e fv_exacta.
Dibuja la solución aproximada y la exacta en la misma figura.

ejercicio1_5

error =
   8.0836e-04

Un bucle while ejecuta un grupo de órdenes mientras que la expresión que controla el bucle sea cierta. La sintaxis es similar a la del for:

%while expresión
%	comandos
%end

Los bucles while y for pueden estar anidados:

t=0;T=1;x=0;
while t<T
    t=t+0.1;
        for i=1:10
            x=x+(i/t);
        end
end
x

x =
   1.6609e+03

Condicionales

La estructura de control if tiene, en su versión más sencilla, la sintaxis:

%if expression
%   statements
%end

Ejemplo 1.7

for k=1:5
    if k^3>30
        disp('k es mayor que 30')
    end
end

k es mayor que 30
k es mayor que 30

Si existen varias opciones usamos:

%if expresión1
%    comandos1
%elseif expresión2
%   comandos2
%else
%   comandos3
%end

Ejercicio 1.6 Escribir un programa llamado nota_final, cuyos argumentos de entrada sean las notas de dos exámenes parciales (parcial1,parcial2) calificados sobre 10. La salida será la nota media. La función imprimirá:

Suspenso si la nota media es menor que 5.
Aprobado si la nota media está entre 5 y 7.
Notable si la nota media está entre 7 y 9.
Sobresaliente si la nota media es mayor o igual que 9.

media=nota_final(3,8)
media=nota_final(8,10)
media=nota_final(6,9)
media=nota_final(2,5)

Aprobado
media =
    5.5000
Sobresaliente
media =
     9
Notable
media =
    7.5000
Suspenso
media =
    3.5000

Ejemplo 1.8 Supongamos que queremos escribir una función que añada una cantidad variable de números. La salida dependerá del número de argumentos de entrada.

(Quitar los "%" al escribir lo siguiente en el fichero addme.m)

%function d = addme(a,b,c)
%
%if nargin==3
%   d=a+b+c;
%elseif nargin==2
%   d=a+b;
%else
%    d=a;
%end

d1=addme(1,5);
fprintf('d=%d\n',d1)
d2=addme(1,5,3);
fprintf('d=%d\n',d2)

d=6
d=9

La orden break finaliza la ejecución de un for o un bucle while. Cuando se encuentra una orden break, la ejecución del programa o función continua con la siguiente orden fuera del bucle.

Ejemplo 1.9

for i=1:5
    if i>3
        break
    end
    i
end

En bucles anidados, break sale solamente del bucle más interno que le contiene:

Ejemplo 1.10

for i=1:5
    for j=1:3
        if i>3 || j==2
            break
        end
    end
     [i j]
end

ans =
     1     2
ans =
     2     2
ans =
     3     2
ans =
     4     1
ans =
     5     1

Ejercicio 1.7 Escribir una función de nombre serie_armonica que calcule la suma \[\sum_{k=1}^{n}\frac{1}{k}=1+\frac{1}{2}+\frac{1}{3}+\cdots+\frac{1}{n}\] Sumaremos términos hasta que \(\frac{1}{n} < tol\). El argumento de entrada será la tolerancia y los argumentos de salida serán la suma y el número de términos que hemos sumado. Tomar tol=0.0174.

Usar bien una combinación for, if para implementar la parada, o unicamente un while

[suma,n]=serie_armonica(0.0174)

suma =
    4.6290
n =
    58

Referencias

Hemos utilizado varias órdenes básicas del Matlab que el lector ya debería conocer. Para más información: Introducción a Matlab

Una introducción al Matlab más exhaustiva (en inglés) se puede encontrar en la página web de Mathworks Getting Started with Matlab