Introducción a procesamiento digital de imágenes con Matlab
Contenidos
En esta serie de prácticas vamos a ilustrar la aplicación al procesamiento digital de imágenes en Matlab de varios métodos numéricos explicados en clase de teoría
En esta práctica introducimos algunos de los aspectos fundamentales de la representación y manipulación de imágenes con Matlab.
Imágenes digitales
Podríamos definir una imagen como una función bidimensional \(f(x,y)\) donde \(x\) e \(y\) son las coordenadas espaciales, y el valor de \(f\) en cualquier par de coordenadas \((x,y)\) es la intensidad de la imagen en dicho punto.
Una imagen puede ser continua con respecto a \(x\) e \(y\), y también en intensidad (imagen analógica). Convertir esta imagen a formato digital requiere que tanto las coordenadas como la intensidad sean digitalizadas. Digitalizar las coordenadas se llama muestrear, mientras que digitalizar la intensidad se denomina cuantización. Entonces, cuando todas las cantidades son discretas, llamamos a la imagen una imagen digital.
Convenciones en el establecimiento de las coordenadas
El resultado de muestrear y cuantizar es una matriz de números reales. El tamaño de la imagen es el número de filas por el número de columnas, \(M\times N\). La indexación de la imagen sigue las convenciones siguientes. La indexación habitual es \[\left( \begin{array}{ccccc} a(0,0) & a(0,1) & \ldots & a(0,N-2) & a(0,N-1)\\ a(1,0) & a(1,1) & \ldots & a(1,N-2) & a(1,N-1) \\ \ldots & \ldots & \ldots & \ldots & \ldots \\ a(M-1,0) & a(M-1,1) & \ldots & a(M-1,N-2) & a(M-1,N-1) \end{array} \right)\ \] Mientras que Matlab indexa de la forma siguiente \[ \left( \begin{array}{ccccc} a(1,1) & a(1,2) & \ldots & a(1,N-1) & a(1,N)\\ a(2,1) & a(2,2) & \ldots & a(2,N-1) & a(2,N) \\ \ldots & \ldots & \ldots & \ldots & \ldots \\ a(M,1) & a(M,2) & \ldots & a(M,N-1) & a(M,N) \end{array} \right)\]
Lectura, visualización y escritura de imágenes.
Matlab soporta los formatos de imagen más habituales. La sintaxis de lectura es
a=imread('lena_gray_512.tif'); whos a
Name Size Bytes Class Attributes a 512x512 262144 uint8
El tipo de dato habitual para una imagen es uint8, es decir, un entero representado en 8 bits. Esto nos da \(2^8=256\) valores que se distribuyen en el rango de \([0,255]\) para cada pixel.
Para la visualización podemos usar imshow, que tiene varias opciones
figure,imshow(a) figure,imshow(a,'InitialMagnification',50,'Border','tight')


Ahora la imagen es una matriz. Podemos extraer porciones de ella. Las órdenes image e imagesc son más flexibles a la hora de visualizar
lena_eye=a(252:284,318:350); figure,imagesc(lena_eye) colormap(gray) axis image % Establece la relación de escala entre ejes % para que los píxeles sean cuadrados title('El ojo derecho de Lena')
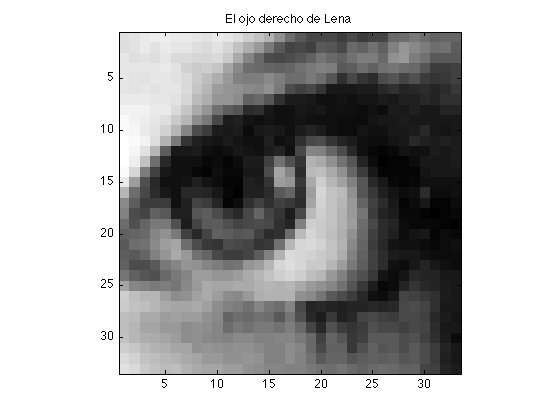
Y podemos guardarlo en el directorio de trabajo usando imwrite
imwrite(lena_eye,'lena_eye.png');
El siguiente comando muestra información de la imagen
imfinfo('lena_gray_512.tif')
ans =
Filename: [1x85 char]
FileModDate: '28-ago-2008 15:03:30'
FileSize: 262598
Format: 'tif'
FormatVersion: []
Width: 512
Height: 512
BitDepth: 8
ColorType: 'grayscale'
FormatSignature: [73 73 42 0]
ByteOrder: 'little-endian'
NewSubFileType: 0
BitsPerSample: 8
Compression: 'Uncompressed'
PhotometricInterpretation: 'BlackIsZero'
StripOffsets: [32x1 double]
SamplesPerPixel: 1
RowsPerStrip: 16
StripByteCounts: [32x1 double]
XResolution: 72
YResolution: 72
ResolutionUnit: 'Inch'
Colormap: []
PlanarConfiguration: 'Chunky'
TileWidth: []
TileLength: []
TileOffsets: []
TileByteCounts: []
Orientation: 1
FillOrder: 1
GrayResponseUnit: 0.0100
MaxSampleValue: 255
MinSampleValue: 0
Thresholding: 1
Offset: 262152
Tipos de imágenes y conversiones
Existen tres tipos principales de imágenes:
- Imagen de intensidad es una matriz de datos cuyos valores han sido escalados para que representen intensidades de una escala de grises. Cuando los elementos de una imagen de intensidad son de clase uint8 (enteros almacenados en 8 bits) o de clase uint16 (enteros almacenados en 16 bits), pueden almacenar, respectivamente, \(2^8=256\) valores en el rango \([0,255]\) o \(2^16=65536\) valores en el rango \([0,65535]\). Si la imagen es de clase double, los valores son números en punto flotante (que se almacenan en 32 bits). En este último caso, los valores se toman en el rango de \([0,1]\) por convención.
- La imagen binaria es una imagen en blanco y negro. Cada pixel tiene asignado un valor lógico de \(0\) ó \(1\).
- La imagen en color es como la imagen de intensidad pero tiene tres canales, es decir, a cada pixel le corresponden tres valores de intensidad (RGB) en lugar de uno.
Cuando realizamos transformaciones matemáticas de imágenes, a menudo necesitamos que la imagen sea de tipo double. Pero cuando la leemos y almacenamos ahorramos espacio usando codificación entera. Podemos usar las órdenes siguientes
- im2uint8: de cualquier tipo a uint8,
- im2double: de cualquier tipo a double,
- im2bw: de cualquier tipo a logical,
- rgb2gray: RGB color a gray.
a1=lena_eye(1:5,1:5) a2=im2double(a1) b1=eye(5) b2=im2bw(b1) whos a1 a2 b1 b2 imagesc(b2)
a1 =
186 188 193 195 197
186 187 193 189 194
190 186 188 186 192
192 190 191 190 193
190 187 189 192 192
a2 =
0.7294 0.7373 0.7569 0.7647 0.7725
0.7294 0.7333 0.7569 0.7412 0.7608
0.7451 0.7294 0.7373 0.7294 0.7529
0.7529 0.7451 0.7490 0.7451 0.7569
0.7451 0.7333 0.7412 0.7529 0.7529
b1 =
1 0 0 0 0
0 1 0 0 0
0 0 1 0 0
0 0 0 1 0
0 0 0 0 1
b2 =
1 0 0 0 0
0 1 0 0 0
0 0 1 0 0
0 0 0 1 0
0 0 0 0 1
Name Size Bytes Class Attributes
a1 5x5 25 uint8
a2 5x5 200 double
b1 5x5 200 double
b2 5x5 25 logical
Ejercicios
Ejercicio 1 Escribir un programa (ejercicio3_1.m) donde
- entrada: una imagen de cualquier tipo y unos determinados rangos para sus píxeles \((x,y)\) Pista: almacenarlos en un solo vector.
- salida: la matriz (tipo double) que corresponda, para los índices dados y una figura que contenga la imagen.
Aplicarlo a seleccionar la cabeza del cameraman en cameraman
p_ejercicio3_1

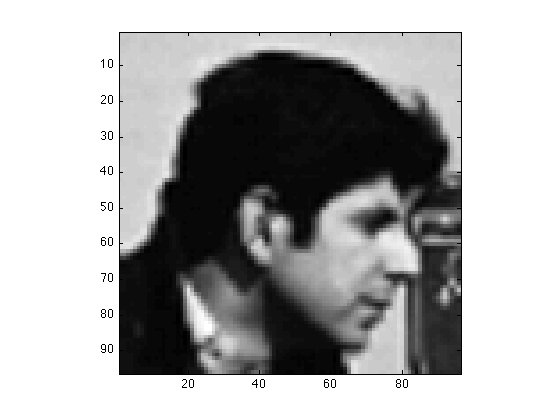

Ejercicio 2 Las máscaras son filtros geométricos de una imagen. Por ejemplo, si queremos seleccionar una región de una image, podemos hacerlo multiplicando la matriz de la imagen original por una matriz de igual tamaño que contenga unos en la región que queremos conservar y cero en el resto. En este ejercicio seleccionamos una región circular de la imagen Lena de radio 150. Seguir los pasos siguientes (fichero ejercicio3_2.m).
- Leer la imagen y convertirla a double.
- Crear una matriz de las mismas dimensiones rellena de ceros.
- Modificar esta matriz de forma que contenga unos en un círculo de radio 150, es decir, si \((i-c_x)^2+(j-c_y)^2<150^2\), con \((c_x,c_y)=(\frac{m}{2},\frac{n}{2})\) como centro de la imagen.
- Multiplicar la imagen por la máscara (recordar que son matrices).
- Mostrar el resultado.
Cuando multiplicas por cero, conviertes a negro los píxeles de fuera del círculo. Modifica el programa para hacer visible esos píxeles con la mitad de su intensidad.
ejercicio3_2

Ejercicio 3 El degradado lineal es un efecto en el que se oscurece una imagen verticalmente (u horizontalmente). Podemos hacer esto con una máscara que sea constante por columnas pero tome un valor decreciente por filas, desde \(1\) en la primera fila a cero en la última. Construir dicha matriz y aplicala a la imagen de Lena.
Pista: puedes usar bucles y comandos if. Pero vectorizar ahorra tiempo de ejecución. Intenta usar las órdenes de Matlab linspace para hacer la degradación y repmat para construir, a partir del vector obtenido con linspace, una matriz.
ejercicio3_3

