Resolución de ecuaciones no lineales

Contenidos

Raíz de una ecuación
Método de bisección
El método de Newton-Raphson
Método de la secante
Orden de convergencia
Comandos Matlab
Ejemplo: una bola que flota
Ejercicio: tiro a la papelera

Raíz de una ecuación

Una ecuación escalar es una expresión de la forma

\[f(x)=0\]

donde \(f:\Omega\subset\mathbb{R}\rightarrow\mathbb{R}\) es una función.

Cualquier número \(\alpha\) tal que \(f(\alpha)=0\) se dice que es una solución de la ecuación o una raíz de \(f\).

Ejemplo 1 Calcular de forma aproximada las raíces de la ecuación:

\[x^3-2x^2+1=0\]

clear,clc,close all,format compact
f=@(x)x.^3-2*x.^2+1;
x=linspace(-1,2);
plot(x,f(x))            % dibujamos la función
hold on
plot([-1 2],[0,0],'k-') % dibujamos el eje X

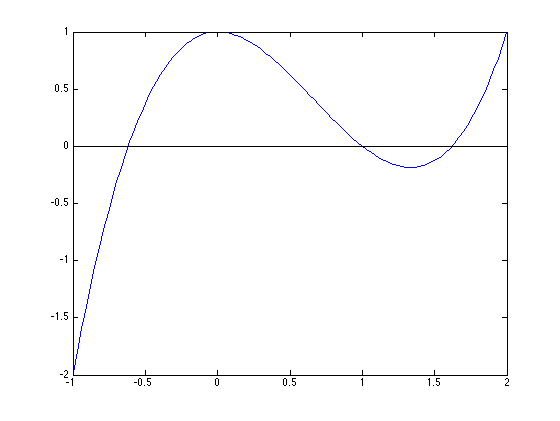
Tiene tres raíces que son, aproximadamente, \(x\simeq -0.6\), \(x\simeq 0.9\) y \(x\simeq 1.6\)

SEPARACIÓN DE RAÍCES

A partir de la gráfica anterior podemos separar las raíces en intervalos que cumplan las condiciones del Teorema de Bolzano:

Sea \(f:[a,b]\rightarrow\mathbb{R}\) una función contínua con \(f(a)f(b)<0\). Entonces existe al menos una raíz de \(f\) en \([a,b]\).

Es decir, buscamos intervalos donde \(f\) tome signos distintos en los extremos.

Y si además la función es monótona creciente o decreciente está garantizado que en el intervalo \([a,b]\) existe una única raíz.

En nuestro ejemplo, tres intervalos que cumplen estas condiciones son:

\[ [-1,-0.1]\quad [0.5,1.1] \quad [1.5,2] \]

Método de bisección

El método de bisección parte de una función \(f\) contínua en un intervalo \([a,b]\) donde se cumplen las condiciones del teorema de Bolzano, es decir, la función tiene distinto signo en los extremos. Para que funcione no es necesario que las raíces estén separadas, pero sí es conveniente (si están las tres raíces en \([a,b]\) sólo aproximará una).

El método de bisección genera una sucesión de intervalos que:

Cumplen las condiciones del teorema de Bolzano.
Y por lo tanto contiene siempre al menos una raíz.
Cada intervalo tiene una longitud que es la mitad del anterior.

En estas condiciones:

La aproximación de la raíz es uno de los extremos del intervalo y por lo tanto
El error máximo cometido es la longitud del intervalo.

ALGORITMO

--Sea \(a_1=a\), \(b_1=b\).
--Para \(k=1,2,\ldots,MaxIteraciones\)
---------Calcular el punto medio \(x_k=\frac{a_k+b_k}{2}\) y evaluar \(f(x_k)\).
---------Si \(x_k\) satisface el criterio de parada, parar.
---------En el caso contrario,
------------------si \(f(a_k)f(x_k)<0\) entonces: \( a_{k+1}=a_{k},\quad b_{k+1}=x_k,\)
------------------en el caso contrario: \( a_{k+1}=x_{k},\quad b_{k+1}=b_k.\)

En el dibujo vemos la sucesión de intervalos (en rojo) para calcular la primera raíz tomando \([a,b]=[-1,0]\).

biseccion

Ejercicio 1. Escribir una función llamada biseccion1 que tenga como argumentos de entrada la función \(f\), los extremos del intervalo \(a\), \(b\) y el número máximo de iteraciones \(n\) y como argumento de salida la solución aproximada.

Si utilizamos la función y los intervalos del ejemplo 1 con 20 iteraciones como máximo:

n=20;a=-1;b=-0.1;     % Datos
x=biseccion1(f,a,b,n) % Aplicamos la función

x =
   -0.6180

a=0.5;b=1.1;          % Datos
x=biseccion1(f,a,b,n) % Aplicamos la función

x =
    1.0000

a=1.5;b=2;            % Datos
x=biseccion1(f,a,b,n) % Aplicamos la función

x =
    1.6180

CRITERIOS DE PARADA

Como la sucesión \(\{x_k\}\) tal que \(x_k\rightarrow \alpha\), con \(f(\alpha)=0\) es, en general, infinita, vamos a introducir un criterio para decidir cuando paramos.

Los criterios de parada se basan en:

El error absoluto \( \left| x_k-x_{k-1}\right| <\epsilon\).
El error relativo \( \frac{\left|x_k-x_{k-1}\right|}{\left|x_k\right|}<\epsilon\).
El residual \( \left|f(x_k)\right|<\epsilon\).

Ejercicio 2. Escribir una función llamada biseccion2 que tenga como argumentos de entrada la función \(f\), los extremos del intervalo \(a\), \(b\) y la cota del error absoluto \(E_a=0.001\) y como argumentos de salida la solución aproximada y el número de iteraciones realizadas.

Ea=0.001;a=-1;b=-0.1;      % Datos
[x,n]=biseccion2(f,a,b,Ea) % Aplicamos la función

x =
   -0.6177
n =
    10

a=0.5;b=1.1;               % Datos
[x,n]=biseccion2(f,a,b,Ea) % Aplicamos la función

a=1.5;b=2;                 % Datos
[x,n]=biseccion2(f,a,b,Ea) % Aplicamos la función

Ejercicio 3. Escribir una función llamada biseccion3 que tenga como argumentos de entrada la función \(f\), los extremos del intervalo \(a\), \(b\) y y la cota del error relativo \(E_r\) y como argumentos de salida la solución aproximada y el número de iteraciones realizadas.

Er=0.001;a=-1;b=-0.1;      % Datos
[x,n]=biseccion3(f,a,b,Er) % Aplicamos la función

x =
   -0.6181
n =
    12

a=0.5;b=1.1;               % Datos
[x,n]=biseccion3(f,a,b,Er) % Aplicamos la función

a=1.5;b=2;                 % Datos
[x,n]=biseccion3(f,a,b,Er) % Aplicamos la función

Ejercicio 4. Escribir una función llamada biseccion4 que que tenga como argumentos de entrada la función \(f\), los extremos del intervalo \(a\), \(b\) y y la cota del residual \(R\) y como argumentos de salida la solución aproximada y el número de iteraciones realizadas.

R=0.001;a=-1;b=-0.1;      % Datos
[x,n]=biseccion4(f,a,b,R) % Aplicamos la función

x =
   -0.6181
n =
    11

a=0.5;b=1.1;              % Datos
[x,n]=biseccion4(f,a,b,R) % Aplicamos la función

a=1.5;b=2;                % Datos
[x,n]=biseccion4(f,a,b,R) % Aplicamos la función

El método de Newton-Raphson

Es el método más usado cuando podemos calcular la derivada exacta.

En cada paso, se sustituye la función por su recta tangente en el punto \(x_k\) y se calcula su raíz, que es una aproximación de la raíz de la función.

ALGORITMO

--Sea \(x_0\) un punto inicial.
--Para \(k=1,2,\ldots,MaxIter\):
---------Calcular \(x_k=x_{k-1}-\frac{f(x_{k-1})}{f'(x_{k-1})}\)
---------Si \(x_k\) satisface el criterio de parada, parar.
---------En el caso contrario, hacer otra iteración.

En el dibujo vemos la sucesión de rectas tangentes (en rojo) para calcular la primera raíz tomando \(x_0=-1\).

Newton

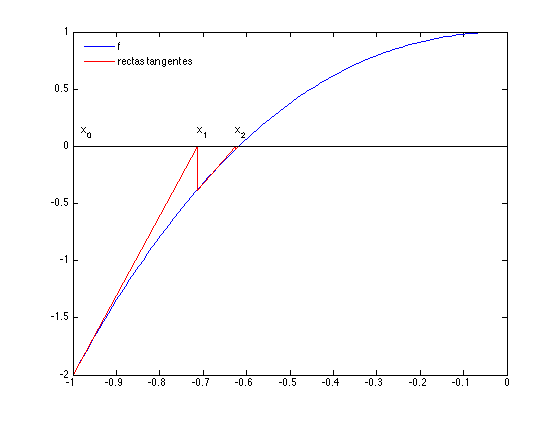
Ejercicio 5 Escribir una función llamada Newton1 que tenga como argumentos de entrada la función \(f\), su derivada \(df\), el punto inicial, el extremo inferior de los intervalos definidos en el ejemplo 1 \(x_0=a\) y la cota de error absoluto \(E_a=0.001\) y como argumento de salida la solución aproximada y el número \(n\) de iteraciones realizadas. Comparar los resultados con los del ejercicio 4.2.

Si utilizamos la función y los intervalos del ejemplo 1:

f=@(x)x.^3-2*x.^2+1; % definimos la función
df=@(x)3*x.^2-4*x;   % definimos su derivada
%
Ea=0.001;x0=-1;           % Datos
[x,n]=Newton1(f,df,x0,Ea) % Aplicamos la función

x =
   -0.6180
n =
     4

x0=0.5;                   % Datos
[x,n]=Newton1(f,df,x0,Ea) % Aplicamos la función

x0=1.5;                   % Datos
[x,n]=Newton1(f,df,x0,Ea) % Aplicamos la función

Método de la secante

Es la variante más importante del método de Netwon-Raphson. Sustituimos la tangente por una secante.

El problema del método de Newton-Raphson es que necesitamos tener la \(f'(x)\).

En el método de la secante aproximamos \(f'(x)\) con diferencias finitas: \[f'(x_{k-1})=\frac{f(x_{k-1})-f(x_{k-2})}{x_{k-1}-x_{k-2}}.\]

Necesitamos dos puntos iniciales, \(x_0\) y \(x_1\) para la primera iteración: \[ x_k= x_{k-1} -f( x_{k-1})\frac{x_{k-1}-x_{k-2}}{f(x_{k-1})-f(x_{k-2})}\]

En el dibujo vemos la sucesión de rectas secantes (en rojo) para calcular la primera raíz tomando \(x_0=0\) y \(x_1=-1\). En verde, la posición de las sucesivas raíces aproximadas.

secante

Ejercicio 6 Escribir una función llamada secante1 que tenga como argumentos de entrada la función \(f\), los puntos iniciales \(x_0\) y \(x_1\), y la cota de error absoluto \(E_a=0.001\) y como argumento de salida la solución aproximada y el número \(n\) de iteraciones realizadas. Comparar los resultados con los del ejercicio 4.2.

Si utilizamos la función y los intervalos del ejemplo 1:

Ea=0.001;x0=-1;x1=-0.1;    % Datos
[x,n]=secante1(f,x0,x1,Ea) % Aplicamos la función

x =
   -0.6180
n =
     7

x0=0.5;x1=1.1;             % Datos
[x,n]=secante1(f,x0,x1,Ea) % Aplicamos la función

x0=1.5;x1=2;               % Datos
[x,n]=secante1(f,x0,x1,Ea) % Aplicamos la función

Orden de convergencia

Los métodos numéricos de cálculo de raíces de una función son métodos iterativos, es decir, si construímos la sucesión \[ x_0,x_1,\ldots,x_k,\ldots\] tal que \[\lim_{k\to\infty}f(x_k)=0.\]

El orden de convergencia de un métodos está relacionado con la velocidad de convergencia de la sucesión con respecto a \(k\).

Este concepto es útil para comparar métodos.

Supongamos que la sucesión \(x_k\) converge a \(\alpha\in\mathbb{R}\). Decimos que \(x_k\) converge a \(\alpha\) con orden de convergencia \(p\) si \[ \lim_{k\to\infty}\frac{|x_k-\alpha|}{|x_{k-1}-\alpha|^p}=\lambda \quad (1) \] Con \(\lambda\) distinto de cero. En los casos particulares

\(p=1\), decimos que la convergencia es lineal \(\rightarrow\) Método de Bisección
\(p=2\), decimos que la convergencia es cuadrática \(\rightarrow\) Método de Newton-Raphson.
\(p\in(1,2)\), decimos que la convergencia es superlineal \(\rightarrow\) Método de la secante \(p=1.618\).

Un método numérico se dice de orden \(p\) si genera una sucesión que converge a la solución con un orden de convergencia \(p\).

Cuanto mayor es el orden de convergencia más rápido converge el método.

Ejercicio 7 Para los tres algoritmos, modificar la función de forma que como argumento de salida nos de, en un vector, todas las soluciones aproximadas que fue calculando. Utilizando la raíz \(\alpha=1\) comprobar que el orden de convergencia de

Método de Bisección es \(p=1\).
Método de Newton-Raphson es \(p=2\).
Método de la Secante es \(p=1.618\).

f=@(x)x.^3-2*x.^2+1;                        % definimos la función
df=@(x)3*x.^2-4*x;                          % definimos su derivada

a=0.5;b=1.1;n=12;                           % Datos
x=biseccion5(f,a,b,n);                      % Aplicamos la función
p=1;                                        % Ahora x es un vector
lambda=abs((x(2:end)-1)./(x(1:end-1)-1).^p) % Calculamos la expresión (1)
figure;plot(lambda,'*-')
xlabel('Iteración'),ylabel('lambda')
% Vemos que tiende a una constante

lambda =
  Columns 1 through 7
    0.2500    0.5000    0.5000    0.5000    0.5000    0.5000    0.5000
  Columns 8 through 11
    0.5000    0.5000    0.5000    0.5000

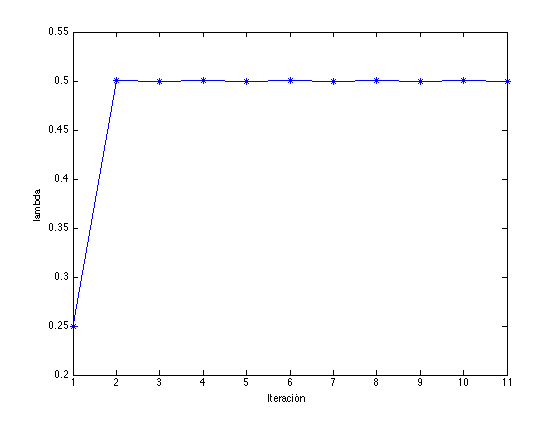
x0=0.02;n=12;                               % Datos
x=Newton2(f,df,x0,n);                       % Aplicamos la función
p=2;                                        % Ahora x es un vector
lambda=abs((x(2:end)-1)./(x(1:end-1)-1).^p) % Calculamos la expresión (1)
figure;plot(lambda,'*-')                     % Vemos que tiende a una constante
xlabel('Iteración'),ylabel('lambda')

lambda =
  Columns 1 through 7
    0.0563    0.0852    0.1293    0.1976    0.3052    0.4782    0.7557
  Columns 8 through 11
    1.1499    1.5023    1.6123    1.6180

x0=0.5;x1=1.5;n=12;                         % Datos
x=secante2(f,x0,x1,n);                      % Aplicamos la función
p=1.618;                                    % Ahora x es un vector
lambda=abs((x(2:end)-1)./(x(1:end-1)-1).^p) % Calculamos la expresión (1)
figure;plot(lambda,'*-')                     % Vemos que tiende a una constante
xlabel('Iteración'),ylabel('lambda')

lambda =
  Columns 1 through 7
    5.0053    0.6251    1.8594    1.6364    1.2564    1.3570    1.3469
  Columns 8 through 11
    1.3463    1.3463    1.3463    1.3463

Comandos Matlab

Podemos calcular las raíces de una ecuación usando el comando Matlab fzero dando como datos la función y un punto próximo a la raíz.

f=@(x)x.^3-2*x.^2+1;

fzero(f,-1)

ans =
   -0.6180

fzero(f,1)

ans =
     1

fzero(f,2)

ans =
    1.6180

El algoritmo que usa es una combinación de los métodos de bisección y secante. Más información sobre este comando (en inglés) en Mathworks-fzero

Si la ecuación es polinómica, el comando roots calcula todas sus soluciones simultáneamente. Como argumento de entrada le daremos los coeficientes del polinomio en un vector.

roots([1 -2 0 1])

ans =
    1.6180
    1.0000
   -0.6180

Ejemplo: una bola que flota

Si depositamos un sólido en la superfície de un líquido, de acuerdo con el teorema de Arquímedes, el sólido se sumergirá hasta una cierta profundidad de forma que el peso del sólido sea igual al peso de fluído desplazado.

Supongamos que tenemos una bola como la de la foto de radio \(R=1\)m y que está sumergida hasta una profundidad \(H\). Determinar cuánto se hunde la bola si el peso de la niña es de \(25\)kg y la bola de plástico pesa \(2\)kg. La densidad del agua es \(\rho_a=1000\)kg/m\(^3\). El error máximo cometido ha de ser de un milímetro.

El volumen sumergido de la esfera es:

\[V=\int_{R-H}^R\pi f(x)^2 dx=\int_{R-H}^R\pi (R^2-x^2)dx=\frac{\pi}{3}(3RH^2-H^3)\] Para \(R=1\)m el volumen es \[V=\frac{\pi}{3}(3H^2-H^3)\] Y el peso del volumen desalojado \[P=V\times \rho_a=V\times1000=25+2\] Y por lo tanto la ecuación a resolver es: \[\frac{\pi}{3}(3H^2-H^3)=0.027\]

f=@(H)pi/3*(3*H.^2-H.^3)-0.027; % definimos la función
df=@(H)pi/3*(6*H-3*H.^2)-0.027; % definimos su derivada

Si resolvemos por el método de bisección:

Ea=0.001;a=0;b=2;          % Datos
[x,n]=biseccion2(f,a,b,Ea) % Aplicamos la función

Es decir, la bola se hunde \(0.094\)m\(=9.4\)cm

Si resolvemos por el método de Newton-Raphson:

Ea=0.001;x0=1;            % Datos
[x,n]=Newton1(f,df,x0,Ea) % Aplicamos la función

Y por el método de la secante:

Ea=0.001;x0=0;x1=2;        % Datos
[x,n]=secante1(f,x0,x1,Ea) % Aplicamos la función

Ejercicio: tiro a la papelera

Tenemos que acertar (con un error pequeñito) a una papelera situada en un punto del eje OX, cuando nosotros nos situamos en el origen y lanzamos un papel con una velocidad y ángulo dado.

Suponemos que nos movemos sólo en el plano y, para dificultar la cosa, hay un viento terrible que, en cada una de las funciones es distinto.

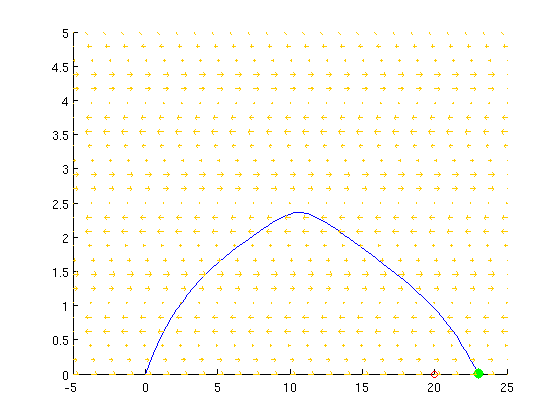
Las funciones de Matlab funcionan del siguiente modo:

Se ejecuta [error,x,y,t] = escenarioX(velocidad,angulo), dándole como argumentos de entrada la velocidad de lanzamiento y el ángulo en grados.
El programa integra la ecuación diferencial numéricamente y, luego, pinta la trayectoria que seguiría el papel cuando lo lanzamos con esa velocidad y ángulo en el escenario de viento elegido.

Las tres funciones Matlab son:

escenario1

escenario2

escenario3

La pregunta es ¿es posible diseñar alguna estrategia para acabar acertando con seguridad a la papelera? ¿en qué casos? Si no podemos hacerlo, ¿por qué puede ser?

NOTA: Calcular la forma vectorial de una función y la de su derivada

Vamos a ver un ejemplo.

Definimos la función en forma simbólica y obtenemos su derivada en forma simbólica.

syms x
f_sim=log((x^2+1)/(x^3+x))*exp(x^3+1)
df_sim=diff(f_sim)

f_sim =
log((x^2 + 1)/(x^3 + x))*exp(x^3 + 1)
df_sim =
3*x^2*log((x^2 + 1)/(x^3 + x))*exp(x^3 + 1) + (exp(x^3 + 1)*((2*x)/(x^3 + x) - ((x^2 + 1)*(3*x^2 + 1))/(x^3 + x)^2)*(x^3 + x))/(x^2 + 1)

A partir de la forma simbólica, definimos la númerica con el comando matlabFunction

f=matlabFunction(f_sim)
df=matlabFunction(df_sim)
clear x f_sim df_sim

f = 
    @(x)log((x.^2+1.0)./(x+x.^3)).*exp(x.^3+1.0)
df = 
    @(x)x.^2.*log((x.^2+1.0)./(x+x.^3)).*exp(x.^3+1.0).*3.0+(exp(x.^3+1.0).*((x.*2.0)./(x+x.^3)-(x.^2+1.0).*(x.^2.*3.0+1.0).*1.0./(x+x.^3).^2).*(x+x.^3))./(x.^2+1.0)