Interpolación aplicada a la transformación de imágenes
Contenidos
Transformaciones lineales
Una aplicación de la interpolación es la transformación lineal también llamada rígida. Si \((i,j)\) es un pixel de la imagen y \(I(i,j)\) su intensidad, una transformación rígida es una transformación lineal de las coordenadas de los pixeles, es decir \[ \left(\begin{array}{cc}p\\q\end{array}\right)= A \left(\begin{array}{cc}i\\j\end{array}\right) \]
donde \(A\) es una matriz \(2\times 2\).
Entre las transformaciones lineales se encuentran el grupo de transformaciones afines, como escalado, rotación y cizallado. Veamos unos ejemplos con Matlab. Para ello, definimos una matriz \(3\times 3\) de la forma \[ \left(\begin{array}{ccc}a_{11} & a_{12} & 0\\a_{21}& a_{22} & 0\\ 0 & 0 & 1\end{array}\right) \] y usamos las órdenens maketform y imtransform con las matrices respectivas: \[\mathrm{Escalado}:\; \left(\begin{array}{ccc}s_1 & 0 & 0\\0& s_2 & 0\\ 0 & 0 & 1\end{array}\right)\qquad \mathrm{Cizallado}:\; \left(\begin{array}{ccc}1 & sh_1 & 0\\sh_2& 1 & 0\\ 0 & 0 &1\end{array}\right) \qquad \mathrm{Rotación}:\; \left(\begin{array}{rrr}\cos(\theta) & -\mathrm{sen}(\theta) & 0\\ \mathrm{sen}(\theta)& \cos(\theta) & 0\\ 0 & 0 & 1\end{array}\right) \] donde \(s_1\) y \(s_2\) son los factores de escala según los ejes \(X\) e \(Y\) respectivamente, \(sh_1\) y \(sh_2\) son los factores de cizalla paralela a los ejes \(X\) e \(Y\) respectivamente y donde \(\theta\) es el ángulo a rotar.
I=imread('cameraman.tif'); I=im2double(I); s=[2,3]; tform1 = maketform('affine',[s(1) 0 0; 0 s(2) 0; 0 0 1]); % Escalado I1 = imtransform(I,tform1); sh=[0.5 0.2]; tform2 = maketform('affine',[1 sh(1) 0; sh(2) 1 0; 0 0 1]); % Cizallado I2 = imtransform(I,tform2); theta=pi/4; % Rotación A=[cos(theta) -sin(theta) 0; sin(theta) cos(theta) 0; 0 0 1]; tform3 = maketform('affine',A); I3 = imtransform(I,tform3); figure imagesc(I),axis image title('Original','FontSize',18) colormap(gray) figure imagesc(I1),axis image title('Escalado','FontSize',18) colormap(gray) figure imagesc(I2),axis image title('Cizallado','FontSize',18) colormap(gray) figure imagesc(I3),axis image title('Girado','FontSize',18) colormap(gray)




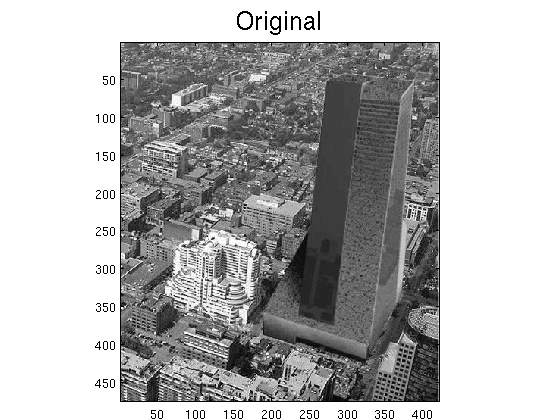
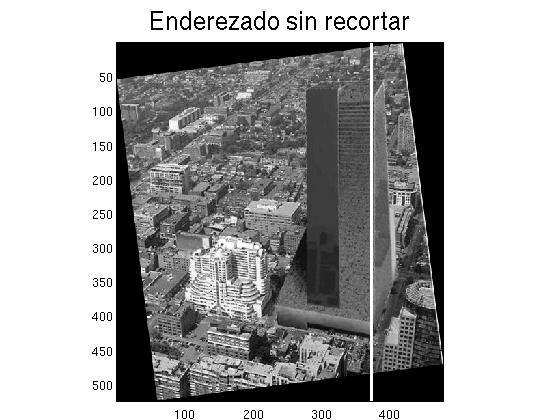
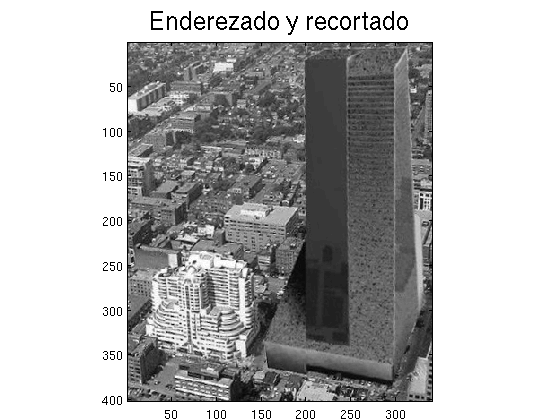
Ejercicio 1 Queremos enderezar la torre de la fotografía tower_bw.jpg. Para ello la tenemos que rotar un ángulo adecuado. Pero una vez rotada, aparece una región negra que no estaba definida. Por lo tanto tenemos que recortar la figura para eliminar esta región.
Escribir un programa que realice estas tareas. Mostrar la imagen inicial, la imagen final y el ángulo rotado (en grados).
Nota: Usar una línea vertical para decidir que la torre está enderezada. Por ejemplo, si la imagen rotada es \(I\), utilizar \(I(:,9:12)=1\) para dibujar una línea blanca vertical que tenga de ancho de la columna 9 a la 12.
Ejercicio1
Transformaciones no lineales
En este caso, en la transformación \[ \left(\begin{array}{cc}p\\q\end{array}\right)= A \left(\begin{array}{cc}i\\j\end{array}\right) \] la matriz \(A\) no tiene que ser la misma para todos los pixeles sino que puede depender del pixel sobre el que está actuando.
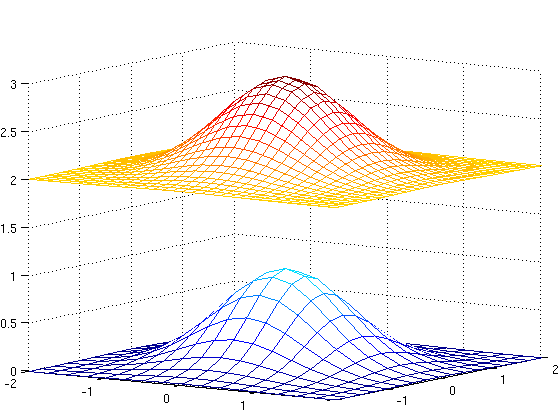
En estas transformaciones se suele usar el comando de Matlab interp2 que interpola funciones en dos dimensiones. Por ejemplo, definimos la función \(f(x,y)=e^{-x^2-y^2}\) en una rejilla gruesa y luego hallamos los valores en los puntos intermedios por interpolación y representamos el resultado:
clear [x,y] = meshgrid(-2:0.25:2); % rejilla gruesa z = exp(-x.^2-y.^2); % para cada punto (x,y) definimos el z de acuerdo con la función [p,q] = meshgrid(-2:0.125:2); % rejilla fina zfinal = interp2(x,y,z,p,q); % interpolamos los puntos intermedios mesh(x,y,z), hold on % dibujamos la superficie utilizando una malla gruesa mesh(p,q,zfinal+2) % dibujamos la superficie utilizando una malla más fina colormap(jet) view([34,10])
La orden interp2 puede usarse también para transformaciones afines. Por ejemplo, podemos si rotamos los píxeles de una imagen alrededor de un punto \((x_0,y_0)\) un ángulo \(\theta\), para cada pixel realizaremos la transformación: \[ \left(\begin{array}{c}p \\ q\end{array}\right)= \left(\begin{array}{cc}\cos(\theta) & \mathrm{sen}(\theta)\\ -\mathrm{sen}(\theta)& \cos(\theta) \end{array}\right) \left(\begin{array}{c}x-x_0 \\ y-y_0\end{array}\right) +\left(\begin{array}{c}x_0 \\ y_0\end{array}\right) \]
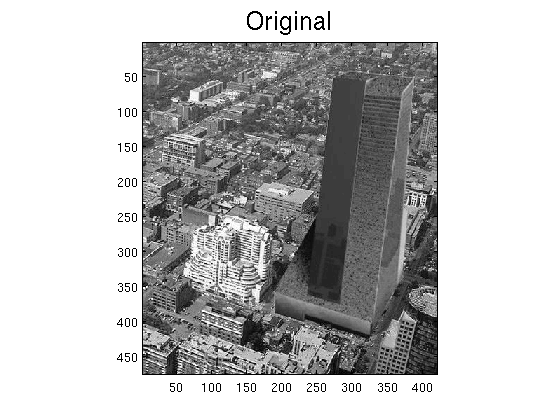
clear I=imread('tower_bw.jpg'); I=im2double(I); m=size(I,1); n=size(I,2); [x,y] = meshgrid(1:n,1:m); % rejilla heredada de la imagen original theta=pi/4; % ángulo de rotación x0=fix(n/2);y0=fix(m/2); % centro de rotación p=(x-x0).*cos(theta)+(y-y0).*sin(theta)+x0; % coordenadas transformadas (nueva posición de los pixeles) q=-(x-x0).*sin(theta)+(y-y0).*cos(theta)+y0; Ifinal=interp2(x,y,I,p,q); % valores de la intensidad interpolada en la nueva posición figure imagesc(I),axis image title('Original','FontSize',18) colormap(gray) figure imagesc(Ifinal),axis image title('Transformada','FontSize',18) colormap(gray)

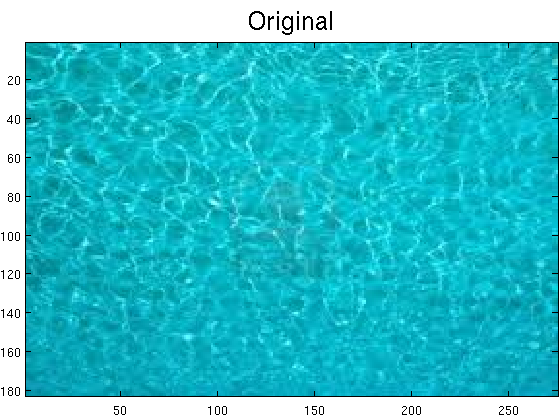
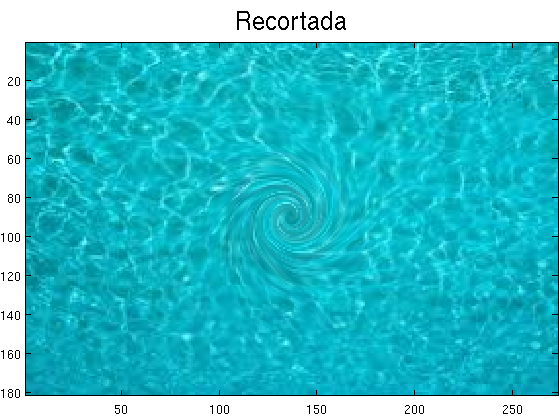
Ejercicio 2 El objetivo de este ejercicio es introuducir un remolino en la piscina, tal como muestra la figura (resultado final del ejercicio)
Ejercicio2
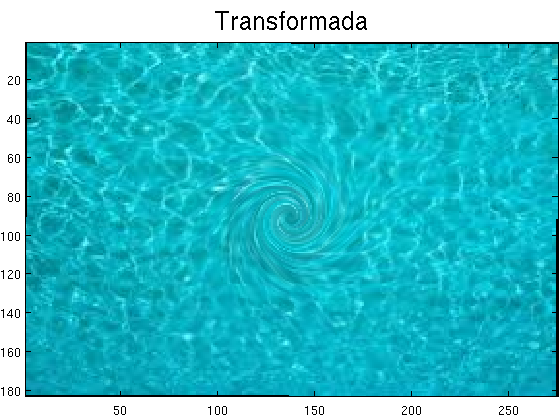
Para realizar este ejercicio, usar la rotación del programa anterior e introducir los siguientes cambios:
- Definir una función en línea \(d=@(x,y)...\) que represente la distancia de un punto cualquiera \((x,y)\) al centro de la imagen \((x_0,y_0)\).
- Definir el ángulo como \( \theta =10*\exp(-0.1*d(x,y))\).
- Definir la posición nueva de cada pixel dependiendo de este ángulo, como en el programa anterior.
- Recortar las líneas negras que aparecen en los bordes.
Si la figura fuera en blanco y negro y tuviéramos sólo una intensidad, usaríamos interp2 como en el programa anterior. Pero como ahora nuestra figura es una imagen rgb, tenemos que realizar la interpolación para cada canal. Lo podemos hacer con un bucle:
%Ifinal=zeros(size(I)); % inicializa la matriz final a ceros %for k=1:3 % tres colores %Ic=I(:,:,k); % selecciona el canal %... %interpola y genera Ic transformado %Ifinal(:,:,k)=Ic; % añade este canal a la matriz de tres capas %end
Recordar que la matriz final tiene ahora tres dimensiones y hay que tenerlo en cuenta al recortarla. Es decir, hemos de usar Ifinal=Ifinal(f1:f2,c1:c2,:);.
Es conveniente devolver la imagen a su formato entero con Ifinal=im2uint8(Ifinal).
Ejercicio 3 El objetivo de este ejercicio es escalar la imagen de forma no uniforme. También se busca automatizar el recortado final.
En este caso definimos la transformación como:
\[ \begin{array}{l} p=0.01*d(x,y).*(x-x0)+x \\ q=0.01*d(x,y).*(y-y0)+y\end{array} \]
Después de la interpolación, obtenemos una figura pequeña rodeada de una gran zona donde la intensidad no está definida. Pero el resultado final debería ser:
Ejercicio3

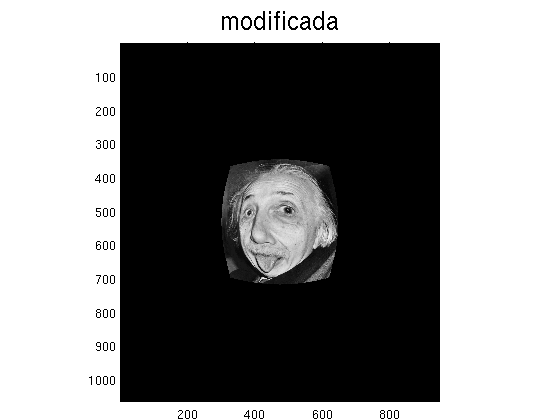

Usando la función find, encontrar los pixeles donde la intensidad interpolada es \( \geq 0\) y definir otra imagen donde solo aparezcan estos píxeles.
Ejercicio 4 Modificar el programa anterior para convertirlo en una función que tenga como argumentos:
- Entrada: una imagen en blanco y negro, el punto central \((x_0,y_0)\).
- Salida: La matriz de la imagen transformada y recortada.
I=imread('einstein_bw.jpg');
A=Ejercicio4(I,361,593);


Ficheros: