Aproximación
Contenidos
Aproximación polinómica discreta
Supongamos que buscamos un polinomio de grado \(2\) que aproxime a la función \(f(x)=\cos(x)\) de la cual solo conocemos los valores en los \(5\) puntos \[x_0=-1,x_1=-0.5,x_2=0,x_3=0.5,x_4=1\] El polinomio será \[P_2(x)=a_0+a_1x+a_2x^2\] Y tendremos tres incógnitas \(a_0,a_1,a_2\),
Las ecuaciones serían \[ \begin{array}{lll} P_{2}(x_{0})=y_{0} & \quad & a_{0}+a_{1}x_{0}+a_{2}x_{0}^{2}=y_{0}\\ P_{2}(x_{1})=y_{1} & \quad & a_{0}+a_{1}x_{1}+a_{2}x_{1}^{2}=y_{1}\\ P_{2}(x_{2})=y_{2} & \quad & a_{0}+a_{1}x_{2}+a_{2}x_{2}^{2}=y_{2}\\ P_{2}(x_{3})=y_{3} & \quad & a_{3}+a_{1}x_{3}+a_{2}x_{3}^{2}=y_{3}\\ P_{2}(x_{4})=y_{4} & \quad & a_{0}+a_{1}x_{4}+a_{2}x_{4}^{2}=y_{4} \end{array} \]
Y el sistema a resolver es: \[ \left(\begin{array}{ccccc} 1 & x_{0} & x_{0}^{2} \\ 1 & x_{1} & x_{1}^{2} \\ 1 & x_{2} & x_{2}^{2} \\ 1 & x_{3} & x_{3}^{2} \\ 1 & x_{4} & x_{4}^{2} \end{array}\right)\left(\begin{array}{c} a_{0}\\ a_{1}\\ a_{2} \end{array}\right)=\left(\begin{array}{c} y_{0}\\ y_{1}\\ y_{2}\\ y_{3}\\ y_{4} \end{array}\right) \]
Tenemos más ecuaciones que incógnitas y el sistema no tiene solución. Pero si multiplicamos los dos miembros por la traspuesta de la matriz de coeficientes: \[ \left(\begin{array}{ccccc} 1 & 1 & 1 & 1 & 1 \\ x_{0} & x_{1} & x_{2} & x_{3}& x_{4}\\ x_{0}^{2} & x_{1}^{2} & x_{2}^{2} & x_{3}^{2} & x_{4}^{2} \end{array}\right) \left(\begin{array}{ccccc} 1 & x_{0} & x_{0}^{2} \\ 1 & x_{1} & x_{1}^{2} \\ 1 & x_{2} & x_{2}^{2} \\ 1 & x_{3} & x_{3}^{2} \\ 1 & x_{4} & x_{4}^{2} \end{array}\right) \left(\begin{array}{c} a_{0}\\ a_{1}\\ a_{2} \end{array}\right)= \left(\begin{array}{ccccc} 1 & 1 & 1 & 1 & 1 \\ x_{0} & x_{1} & x_{2} & x_{3}& x_{4}\\ x_{0}^{2} & x_{1}^{2} & x_{2}^{2} & x_{3}^{2} & x_{4}^{2} \end{array}\right) \left(\begin{array}{c} y_{0}\\ y_{1}\\ y_{2}\\ y_{3}\\ y_{4} \end{array}\right) \]
Y ahora tenemos un sistema determinado de \(3\) ecuaciones con \(3\) incógnitas: \[ \left(\begin{array}{ccc} n+1 & \sum_{k=0}^{n}x_{k} & \sum_{k=0}^{n}x_{k}^{2}\\ \sum_{k=0}^{n}x_{k} & \sum_{k=0}^{n}x_{k}^{2} & \sum_{k=0}^{n}x_{k}^{3}\\ \sum_{k=0}^{n}x_{k}^{2} & \sum_{k=0}^{n}x_{k}^{3} & \sum_{k=0}^{n}x_{k}^{4} \end{array}\right)\left(\begin{array}{c} a_{0}\\ a_{1}\\ a_{2} \end{array}\right)=\left(\begin{array}{c} \sum_{k=0}^{n}y_{k}\\ \sum_{k=0}^{n}x_{k}y_{k}\\ \sum_{k=0}^{n}x_{k}^{2}y_{k} \end{array}\right) \]
Ejercicio 1 Escribir una función V=Vandermonde2(x,g) que tenga como entrada el vector x y el grado del polinomio de aproximación g y que calcule la matriz V. Utilizarla para hallar el polinomio de aproximación a los puntos x, y. Dibujar los puntos con el polinomio de aproximación. \[V= \left(\begin{array}{ccccc} 1 & x_{0} & x_{0}^{2} \\ 1 & x_{1} & x_{1}^{2} \\ 1 & x_{2} & x_{2}^{2} \\ 1 & x_{3} & x_{3}^{2} \\ 1 & x_{4} & x_{4}^{2} \end{array}\right) \]
x=[-1,-0.5,0,0.5,1]; y=cos(x); V=Vandermonde2(x,2)
V =
1.0000 -1.0000 1.0000
1.0000 -0.5000 0.2500
1.0000 0 0
1.0000 0.5000 0.2500
1.0000 1.0000 1.0000
a=V'*V\V'*y' aa=a(end:-1:1)'
a =
0.9949
0
-0.4554
aa =
-0.4554 0 0.9949
xx=linspace(min(x),max(x)); yy=polyval(aa,xx); plot(x,y,'o',xx,yy,'r-') legend('puntos','función aproximada','location','south')

Podemos obtener el polinomio con la orden polyfit dándole el grado del polinomio de aproximación.
a2=polyfit(x,y,2)
a2 = -0.4554 0.0000 0.9949
Aproximación polinómica continua
Pero si en lugar de conocer solo algunos puntos de la función conocemos la función completa en un intervalo podemos hacer el ajuste contínuo. En este caso, los sumatorios se convierten en integrales: \[ \left(\begin{array}{ccc} \int_{-1}^{1}1 dx & \int_{-1}^{1}x dx & \int_{-1}^{1}x^2 dx\\ \int_{-1}^{1}x dx & \int_{-1}^{1}x^2 dx & \int_{-1}^{1}x^3 dx\\ \int_{-1}^{1}x^2 dx & \int_{-1}^{1}x^3 dx & \int_{-1}^{1}x^4 dx \end{array}\right)\left(\begin{array}{c} a_{0}\\ a_{1}\\ a_{2} \end{array}\right)=\left(\begin{array}{c} \int_{-1}^{1}f(x)dx\\ \int_{-1}^{1}x f(x)dx\\ \int_{-1}^{1}x^2 f(x)dx \end{array}\right) \]
Construímos la matriz de coeficientes el vector de términos independientes
gr=2; % grado del polinomio A=zeros(gr+1,gr+1); % matriz de coeficientes b=zeros(gr+1,1); % término independiente for i=1:gr+1 for j=1:gr+1 exponente=i+j-2; integrando_A=@(x)x.^exponente; A(i,j)=quad(integrando_A,-1,1); % integramos numéricamente end integrando_b=@(x)(x.^(i-1)).*cos(x); b(i,1)=quad(integrando_b,-1,1); end
Resolvemos el sistema
sol=A\b; sol=sol(end:-1:1)'
sol = -0.4653 -0.0000 0.9966
Dibujamos juntas la función coseno y su función aproximada
xx=linspace(-1,1); yy=polyval(sol,xx); plot(xx,cos(xx),xx,yy,'r-') legend('función exacta','función aproximada','location','south')

Una aproximación del error relativo será
Er=norm(cos(xx)-yy)/norm(cos(xx))
Er =
0.0037
Ejercicio 2 Dada la función \(f(x)=\cos(\arctan(x))-\log(x+2)\exp(x^2)\), calcular la aproximación polinómica de \(f\) de grado 4. Dar los coeficientes, el error relativo y dibujar la función y la aproximación polinómica como en el ejemplo anterior.
Ejercicio2
Coeficientes del polinomio (de mayor a menor grado):
sol =
-0.0812 -1.0312 -1.0031 -0.3821 0.3041
Error relativo:
Er =
0.0332

Aproximación con polinomios ortogonales
Si suponemos que hemos estado usando el producto escalar de funciones
\[ \left\langle f(x),g(x)\right\rangle=\int_{-1}^ 1 f(x)g(x)dx\] y la base de polinomios \(\{P_0,P_1,P_2\}=\{1,x,x^2\}\) podemos reescribir el sistema como \[ \left(\begin{array}{ccc} \left\langle P_0,P_0\right\rangle & \left\langle P_0,P_1\right\rangle & \left\langle P_0,P_2\right\rangle\\ \left\langle P_1,P_0\right\rangle & \left\langle P_1,P_1\right\rangle & \left\langle P_1,P_2\right\rangle\\ \left\langle P_2,P_0\right\rangle & \left\langle P_2,P_1\right\rangle & \left\langle P_2,P_2\right\rangle \end{array}\right)\left(\begin{array}{c} a_{0}\\ a_{1}\\ a_{2} \end{array}\right)=\left(\begin{array}{c} \left\langle P_0,f(x)\right\rangle\\ \left\langle P_1,f(x)\right\rangle\\ \left\langle P_2,f(x)\right\rangle \end{array}\right) \]
Podemos mejorar el método anterior si conseguimos que la matriz de coeficientes sea diagonal. Lo conseguiríamos si tuviéramos una base de polinomios ortogonales \(\{L_0,L_1,L_2\}\). Entonces se tendría \[ \left(\begin{array}{ccc} \left\langle L_0,L_0\right\rangle & 0 & 0\\ 0& \left\langle L_1,L_1\right\rangle & 0\\ 0 & 0 & \left\langle L_2,L_2\right\rangle \end{array}\right)\left(\begin{array}{c} a_{0}\\ a_{1}\\ a_{2} \end{array}\right)=\left(\begin{array}{c} \left\langle L_0,f(x)\right\rangle\\ \left\langle L_1,f(x)\right\rangle\\ \left\langle L_2,f(x)\right\rangle \end{array}\right) \] Y ahora tenemos que \[ a_0=\frac{\left\langle L_0,f(x)\right\rangle}{\left\langle L_0,L_0\right\rangle} \quad a_1=\frac{\left\langle L_1,f(x)\right\rangle}{\left\langle L_1,L_1\right\rangle} \quad a_2=\frac{\left\langle L_2,f(x)\right\rangle}{\left\langle L_2,L_2\right\rangle} \] Estos polinomios existen y son los Polinomios de Legendre \[L_0(x)=\frac{1}{2},\quad L_1(x)=x,\quad L_2(x)=\frac{1-3x^ 2}{2}.\]
Si resolvemos el problema anterior usando los polinomios ortogonales, obtenemos el mismo resultado.
n=@(x)(1/2)*cos(x); d=@(x)(1/2)^2-x+x; sol(1)=quad(n,-1,1)/quad(d,-1,1); % n=@(x)x.*cos(x); d=@(x)(x.^2); sol(2)=quad(n,-1,1)/quad(d,-1,1); % n=@(x)1/2*(1-3*x.^2).*cos(x); d=@(x)1/4*(1-3*x.^2).^2; sol(3)=quad(n,-1,1)/quad(d,-1,1); a=sol % pol=@(x)sol(1)*(1/2)+sol(2)*x+sol(3)*1/2*(1-3*x.^2); % xx=linspace(-1,1); % plot(xx,cos(xx),xx,pol(xx),'r-') legend('función exacta','función aproximada','location','south')
a =
1.6829 0.0000 0.3102 -0.3821 0.3041

Una aproximación del error relativo será
Er=norm(cos(xx)-pol(xx))/norm(cos(xx))
Er =
0.0037
Ejercicio 3 El tercer y cuarto polinomios de Legendre son: \[L_3(x)=\frac{5x^3-3x}{2},\quad L_4(x)=\frac{35x^4-30x^2+3}{8}.\] Dada la función \(f(x)=\cos(\arctan(x))-\log(x+2)\exp(x^2)\), calcular:
- La aproximación polinómica de \(f\) de grado 4, \(q\). Dar los coeficientes, el error relativo y dibujar la función y la aproximación polinómica como en el ejemplo anterior.
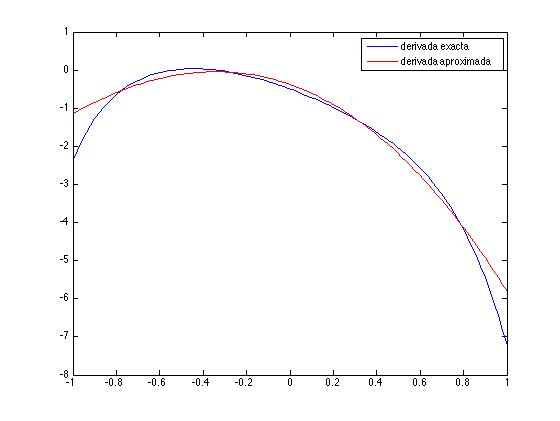
- Calcular las derivadas de \(f\) y \(q\), dar el error relativo y dibujarlas juntas.
Ejercicio3
Coeficientes:
a =
-0.0465 -1.0008 0.7152 -0.4125 -0.0186
Error relativo entre funciones:
Er =
0.0332
Error relativo entre derivadas:
Erd =
0.1461

Nota A continuación un ejemplo de cómo derivar una función simbólica y de cómo convertir las funciones simbólicas en funciones en línea.
syms x % declaramos la variable simbólica x f_sim=cos(atan(x))-log(x+2)*exp(x^2) % definimos la función simbólicamente df_sim=diff(f_sim) % la derivamos f=matlabFunction(f_sim) % transformamos ambas en funciones en línea df=matlabFunction(df_sim) clear x f_sim df_sim % borramos las variables y funciones simbólicas
f_sim =
1/(x^2 + 1)^(1/2) - log(x + 2)*exp(x^2)
df_sim =
- x/(x^2 + 1)^(3/2) - exp(x^2)/(x + 2) - 2*x*log(x + 2)*exp(x^2)
f =
@(x)1.0./sqrt(x.^2+1.0)-log(x+2.0).*exp(x.^2)
df =
@(x)-x.*1.0./(x.^2+1.0).^(3.0./2.0)-exp(x.^2)./(x+2.0)-x.*log(x+2.0).*exp(x.^2).*2.0
Aproximación con funciones trigonométricas: Fourier
Si \(f\) es una función periódica de periodo \(T\) la aproximación mediante funciones trigonométricas resulta especialmente adeduada. Utilizaríamos el producto escalar
\[ \left\langle f(x),g(x)\right\rangle=\int_{\lambda}^{\lambda+T} f(x)g(x)dx\] donde el intervalo de integración es un intervalo que abarca un periodo completo.
La base de funciones trigonométricas \[ \left\{ 1,\cos\left(\frac{2\pi x}{T}\right),\mathrm{sen} \left(\frac{2\pi x}{T}\right),\cos\left(2\frac{2\pi x}{T}\right),\mathrm{sen} \left(2\frac{2\pi x}{T}\right),\ldots,\cos\left(n\frac{2\pi x}{T}\right),\mathrm{sen} \left(n\frac{2\pi x}{T}\right)\right\} \] que es una base ortogonal para el producto escalar dado. Entonces, podemos escribir el sistema
\[ \left(\begin{array}{cccccc} \int_{\lambda}^{\lambda+T} 1^2 dx & 0 & 0 & \cdots & 0 & 0\\ 0& \int_{\lambda}^{\lambda+T} \cos^2\left(\frac{2\pi x}{T}\right) dx & 0& \cdots & 0 & 0\\ 0 & 0 & \int_{\lambda}^{\lambda+T} \mathrm{sen}^2 \left(\frac{2\pi x}{T}\right) dx & \cdots & 0 & 0\\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots\\ 0 & 0 & 0 & \cdots & \int_{\lambda}^{\lambda+T} \cos^2 \left(n\frac{2\pi x}{T}\right) dx & 0\\ 0 & 0 & 0 & \cdots & 0 & \int_{\lambda}^{\lambda+T} \mathrm{sen}^2 \left(n\frac{2\pi x}{T}\right) dx\\ \end{array}\right)\left(\begin{array}{c} \frac{a_{0}}{2}\\ a_{1}\\ b_{1}\\ \cdots\\ a_{n}\\ b_{n} \end{array}\right)=\left(\begin{array}{c} \int_{\lambda}^{\lambda+T} f(x) dx\\ \int_{\lambda}^{\lambda+T} f(x)\cos \left(\frac{2\pi x}{T}\right) dx\\ \int_{\lambda}^{\lambda+T} f(x)\mathrm{sen} \left(\frac{2\pi x}{T}\right) dx\\ \cdots\\ \int_{\lambda}^{\lambda+T} f(x)\cos \left(n\frac{2\pi x}{T}\right) dx\\ \int_{\lambda}^{\lambda+T} f(x)\mathrm{sen} \left(n\frac{2\pi x}{T}\right) dx \end{array}\right) \] Y la función que aproximaría a \(f\) sería de la forma: \[ F(x)=\frac{a_0}{2}+a_1\cos\left(\frac{2\pi x}{T}\right)+b_1\mathrm{sen} \left(\frac{2\pi x}{T}\right)+a_2\cos\left(2\frac{2\pi x}{T}\right)+b_2\mathrm{sen} \left(2\frac{2\pi x}{T}\right)+\cdots+a_n\cos\left(n\frac{2\pi x}{T}\right)+b_n\mathrm{sen} \left(n\frac{2\pi x}{T}\right) \] Y ahora tenemos que \[ \frac{a_0}{2}=\frac{\int_{\lambda}^{\lambda+T} f(x) dx}{\int_{\lambda}^{\lambda+T} 1^2 dx} \quad a_1=\frac{\int_{\lambda}^{\lambda+T} f(x)\cos \left(\frac{2\pi x}{T}\right) dx}{\int_{\lambda}^{\lambda+T} \cos^2\left(\frac{2\pi x}{T}\right)dx} \quad b_1=\frac{\int_{\lambda}^{\lambda+T} f(x)\mathrm{sen} \left(\frac{2\pi x}{T}\right) dx}{\int_{\lambda}^{\lambda+T} \mathrm{sen}^2\left(\frac{2\pi x}{T}\right)dx} ,\ldots, a_n=\frac{\int_{\lambda}^{\lambda+T} f(x)\cos \left(n\frac{2\pi x}{T}\right) dx}{\int_{\lambda}^{\lambda+T} \cos^2\left(n\frac{2\pi x}{T}\right)dx} \quad b_n=\frac{\int_{\lambda}^{\lambda+T} f(x)\mathrm{sen} \left(n\frac{2\pi x}{T}\right) dx}{\int_{\lambda}^{\lambda+T} \mathrm{sen}^2\left(n\frac{2\pi x}{T}\right)dx} \]
Como se tiene que
\[ \int_{\lambda}^{\lambda+T} 1^2 dx= T, \quad \int_{\lambda}^{\lambda+T} \cos^2\left(k\frac{2\pi x}{T}\right)dx = \frac{T}{2}, \quad \int_{\lambda}^{\lambda+T} \mathrm{sen}^2\left(k\frac{2\pi x}{T}\right)dx = \frac{T}{2} \]
para cualquier \(k\) entero positivo, los coeficientes de las funciones de la base serán
\[ a_0=\frac{2}{T}\int_{\lambda}^{\lambda+T} f(x) dx, \quad a_1=\frac{2}{T}\int_{\lambda}^{\lambda+T} f(x) \cos\left(\frac{2\pi x}{T}\right) dx, \quad b_1=\frac{2}{T}\int_{\lambda}^{\lambda+T} f(x)\mathrm{sen} \left(\frac{2\pi x}{T}\right) dx, \ldots, a_n=\frac{2}{T}\int_{\lambda}^{\lambda+T} f(x)\cos \left(n\frac{2\pi x}{T}\right) dx, \quad b_n=\frac{2}{T}\int_{\lambda}^{\lambda+T} f(x)\mathrm{sen} \left(n\frac{2\pi x}{T}\right) dx. \]
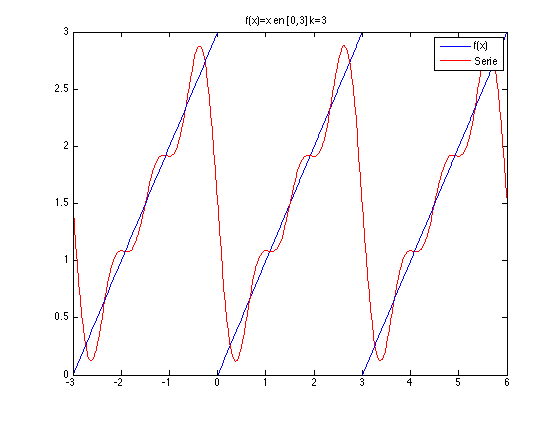
Ejemplo 4 Dibujar la serie de Fourier desde el término 1 hasta el término 10 para la función \(f(x)=x\) en el intervalo \([0,3]\) de periodo \(T=3\).
close all f=@(x)x; % funcion aa=0;bb=3; % intervalo n=10; % numero de iteraciones T=bb-aa; % periodo f1=@(x)f(x+T); % definimos la función f en el periodo anterior f2=@(x)f(x-T); % definimos la función f en el periodo siguiente % a=zeros(1,n); b=zeros(1,n); xx=linspace(aa,bb); xx1=linspace(aa-T,bb-T); xx2=linspace(aa+T,bb+T); xxt=linspace(aa-T,bb+T,300); a0=quad(f,aa,bb)/T; s=a0*ones(1,length(xxt)); for k=1:n figure(k) hold on % calculamos ak y bk fun1=@(x)cos(2*pi*k*x/T).*f(x); fun2=@(x)sin(2*pi*k*x/T).*f(x); a(k)=2*quad(fun1,aa,bb)/T; b(k)=2*quad(fun2,aa,bb)/T; % calculamos el término y lo sumamos a la serie s1=a(k)*cos(2*pi*k*xxt/T)+b(k)*sin(2*pi*k*xxt/T); s=s+s1; % dibujamos la función plot(xx,f(xx)) % dibujamos los términos de la serie de Fourier plot(xxt,s,'r') legend('f(x)','Serie') % dibujamos otros dos periodos de la función plot(xx1,f1(xx-T)) plot(xx2,f2(xx+T)) title(['f(x)=x en [0,3] k=',num2str(k)]) box on end









Ejercicio Dibujar la serie de Fourier desde el término 1 hasta el término 6 para la función \(f(x)=(x-\pi)^2\) en el intervalo \([0,2\pi]\) de periodo \(T=2\pi\).
Ejercicio4





