Aproximación de Fourier. Aplicaciones al procesamiento digital de imágenes.
Contenidos
Introducción: Transformada de Fourier en una dimensión (1D)
Sea \(f(t)\) una señal discreta en una dimensión (1D), periódica en \((0, T) \) y supongamos que se ha muestreado con una frecuencia de muestreo \(fs\), es decir, hemos capturado \(fs\) muestras de la señal cada segundo. Los instantes en que muestreamos son entonces \[ t_n=\frac{n}{fs}, \quad\text{for}\quad n=0,1,\ldots, N-1\] siendo \(N=[Tfs]+1\). La Transformada Discreta de Fourier (Discrete Fourier Transform, DFT, en inglés) de \(f\) se denota con \(F \) y viene dada por \[ F(n)= \frac{1}{\sqrt{N}}\sum_{k=0}^{N-1} f(t_n) \exp(-\frac{2\pi i n k}{N})\] La transformada de Fourier nos permite identificar las componentes frecuenciales de la señal. Estas se corresponden con los valores del módulo al cuadrado de \(F\), es decir, \(P(n)= F(n)\bar F(n)\) donde \(\bar F\) denota la conjugada compleja de \(F\) y \(P(n)\) es el espectro de potencia de la señal \(f\).
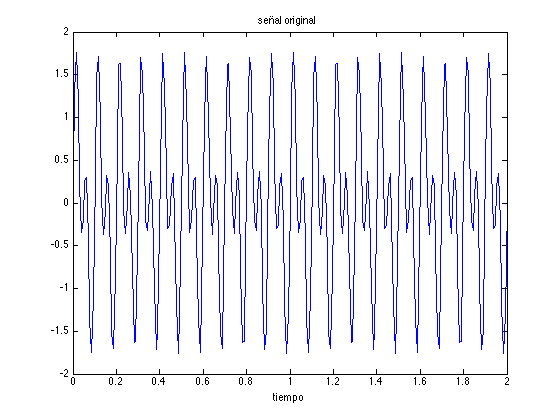
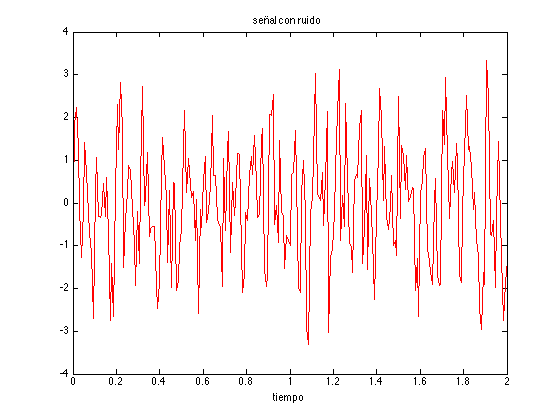
Ejemplo 1. Calculamos los espectros de potencia de una curva sinusoidal compuesta por las frecuencias 10 y 20 Hz, y de la misma señal corrompida con ruído.
T=2; % periodo de muestreo fs=128; % frecuencia de muestreo t=[0:1/fs:T]; % puntos de muestreo N=length(t); f=sin(10*2*pi*t)+sin(20*2*pi*t); % señal original g=f+randn(size(f)); % señal con ruído figure, plot(t,f), xlabel('tiempo'), title('señal original') figure, plot(t,g,'r'), xlabel('tiempo'), title('señal con ruido')
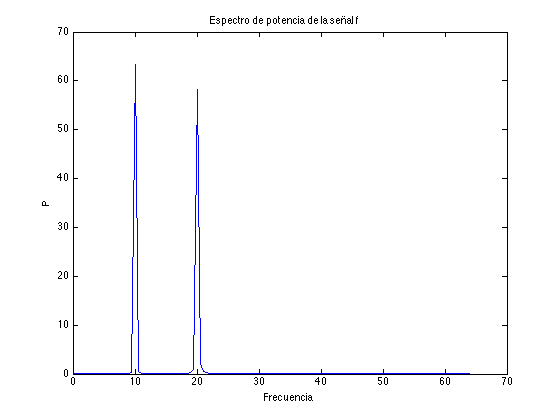
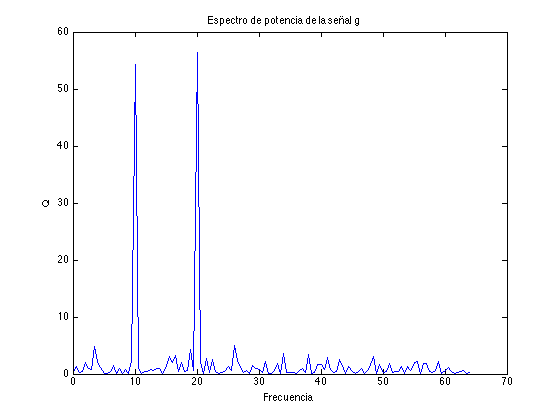
F=fft(f)/sqrt(N); % trasformada de Fourier de f G=fft(g)/sqrt(N); % trasformada de Fourier de g % Para dibujarlo, despreciamos la mitad del dominio debido a la simetría omega=0.5*fs*linspace(0,1,floor(N/2)+1); % vector de frecuencias discretas range=(1:floor(N/2)+1); % rango del espectro de potencia P=abs(F(range)).^2; % espectro de potencia de la señal f Q=abs(G(range)).^2; % espectro de potencia de la señal g figure, plot(omega,P), xlabel('Frecuencia'), ylabel('P'),title('Espectro de potencia de la señal f') figure, plot(omega,Q), xlabel('Frecuencia'), ylabel('Q'),title('Espectro de potencia de la señal g')
La transformada de Fourier tiene un camino de vuelta: la transformada inversa de Fourier. Dada una función \(F\) definida en el dominio de frecuencias de la transformada inversa de Fourier, tiene una definición similar a la definición de la directa: simplemente hay que cambiar el signo dentro de la exponencial.
La propiedad más importante de la transformada inversa es la siguiente. Sea \(F\) la transformada de Fourier de la señal \(f\). Entonces \[ f(t_n)=\frac{1}{\sqrt{N}}\sum_{k=0}^{N-1} F(n) \exp(\frac{2\pi i n k}{N} )\]
Ejemplo 2. Una forma sencilla de quitar el ruído a una señal es el método del valor umbral (en inglés thresholding). Consiste en hacer cero algunos de los coeficientes de Fourier, por ejemplo, aquellos que son pequeños, y entonces aplicar la transformada inversa de Fourier.
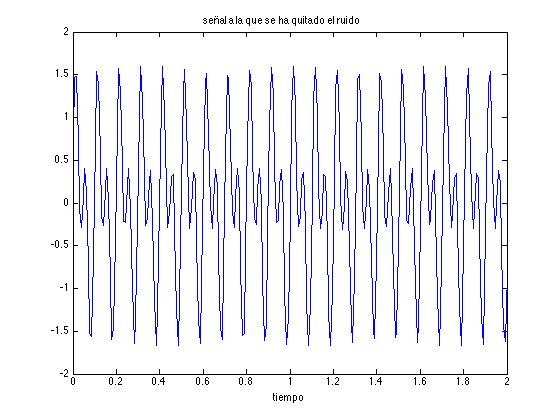
Q2=G.*conj(G); % Calculamos el espectro de potencia para todo el rango de valores GT=G.*(Q2>10); % Hacemos cero los coeficientes con valores del espectro de potencia % por debajo de 10 (los escojemos a partir de la % figura del espectro de potencia) gT=ifft(GT)*sqrt(N); % Aplicamos la transformada inversa de Fourier figure, plot(t,gT), xlabel('tiempo') , title('señal a la que se ha quitado el ruido')
Una versión resumida del código anterior
% Definimos la señal con ruido T=2; fs=128; t=[0:1/fs:T]; N=length(t); g=sin(10*2*pi*t)+sin(20*2*pi*t)+randn(1,N); % Obtenemos la transformada y calculamos su módulo al cuadrado G=fft(g)/sqrt(N); Q=abs(G).^2; % En la transformada, eliminamos los elementos con módulo al cuadrado menores que 10 GT=G.*(Q > 10); % Obtenemos la antitrasformada del espectro de potencias "limpiado" gT=ifft(GT)*sqrt(N ); % Dibujamos la señal original y la procesada figure, plot(t,g,'r'), xlabel('tiempo') , title('señal original') figure, plot(t,gT), xlabel('tiempo') , title('señal a la que se ha quitado el ruido')
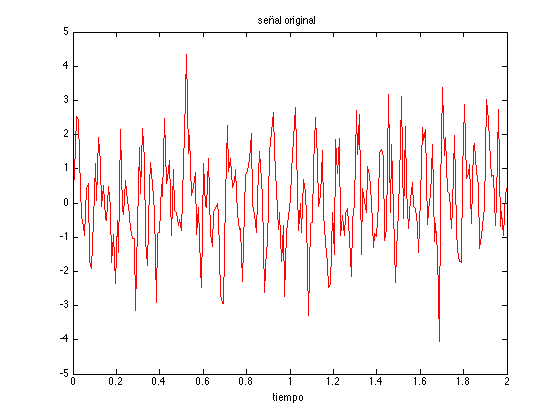
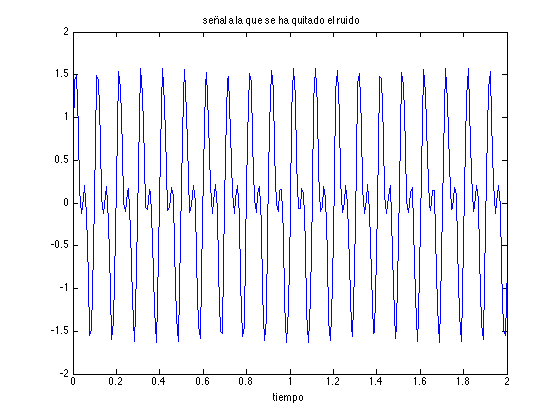
Ejercicio 1. Usar la técnica descrita para quitar el ruído al fichero de audio flauta_noise.wav.
Tener en cuenta las siguientes funciones Matlab:
- [f,fs]=wavread('input.wav'), guarda el fichero input.wav en f y su frecuencia de muestreo es fs.
- wavwrite(f,fs,'output.wav'), guarda el vector f en el fichero de salida output.wav con una frecuencia de muestreo fs.
- sound(f,fs), reproduce el fichero f con una frecuencia de muestreo fs (hacen falta auriculares para oirlo).
Transformada de Fourier en dos dimensiones (2D)
Sea \(f(x,y)\) una imagen \(M\times N\), para \(x=0,1,2,\ldots,M-1\) y \(y=0,1,2,\ldots,N-1\). La Transformada Discreta de Fourier, (Discrete Fourier Transform, DFT, en inglés), en 2D de \(f\), dada por \(F(m,n) \), viene dada por \[ F(m,n)= \sum_{x=0}^{M-1}\sum_{y=0}^{N-1} f(x,y) \exp(-2\pi i(\frac{x}{M}m+\frac{y}{N}n))\] para \(m=0,1,2,\ldots,M-1\) y \(n=0,1,2,\ldots,N-1\).
La region rectangular \(M\times N\) definida por \( (m,n)\) se llama el dominio de frecuencias, y los valores de \(F(m,n)\) se llaman Coeficientes de Fourier.
La inversa de la transformada de Fourier discreta viene dada por \[ f(x,y)=\frac{1}{MN}\sum_{m=0}^{M-1}\sum_{n=0}^{N-1} F(m,n) \exp(2\pi i(\frac{m}{M}x+\frac{n}{N}y)),\] para \(x=0,1,2,\ldots,M-1\) y \(y=0,1,2,\ldots,N-1\).
Nota En algunas formulaciones de la DFT, el término \(1/MN\) se coloca delante de la transformada y en otras se usa delante de la inversa. En otras se utiliza en ambas el término \(1/\sqrt{MN}\). Para ser consistentes con Matlab hemos colocado este término delante de la inversa. Recordar también que los índices en Matlab empiezan con \(1\) y no con \(0\).
Incluso si \(f(x,y)\) es real, su transformada \(F(m,n)\) es en general una función compleja. El espectro de potencia es \(P(m,n)= F(m,n) \bar F(m,n)\), donde \(\bar F\) es la conjugada compleja de \(F\).
Dos propiedades
- Tanto la imagen \(f\) como su DFT son periódicas: \[ f(x,y)=f(x+M,y+M),\quad F(m,n)=F(m+M,n+N) \]
- El espectro de potencia es simétrico respecto al origen: \[ P(m,n)=P(-m,-n) \]
Gracias a estas propiedades, podemos representar la DFT en un cuadrado centrado en \( (0,0) \).
- La DFT y su inversa se obtienen en la práctica usando la transformada rápida de Fourier (Fast Fourier Transformm, fft). En Matlab esto se consigue con la orden fft2:|F=fft2(f)|.
- Para calcular el espectro de potencia, usamos la función de Matlab abs: P=abs(F)^2.
- Si queremos mover el origen de la transformada al centro del rectángulo de frecuencias usamos Fc=fftshift(F).
- Si queremos visualizar mejor los resultados usamos una escala logarítmica.
Ejemplos
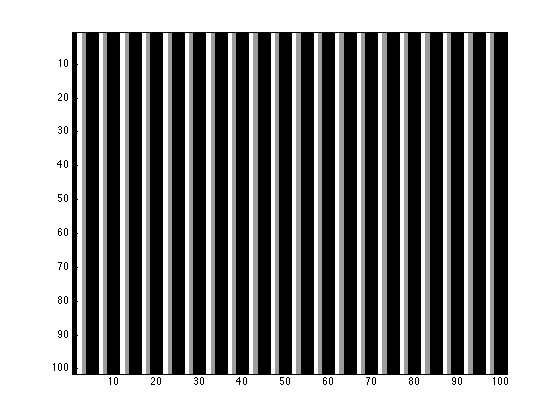
Ejemplo 3. Cargamos la imagen periódica en la dirección horizontal lines.tif
- En la primera figura vemos la imagen.
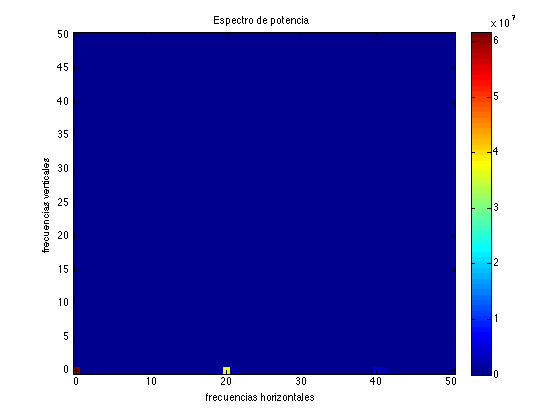
- La segunda figura corresponde al espectro de potencia, P, de la imagen. Aparece un máximo en \((0,20)\) que se visualiza como un rectángulo amarillo.
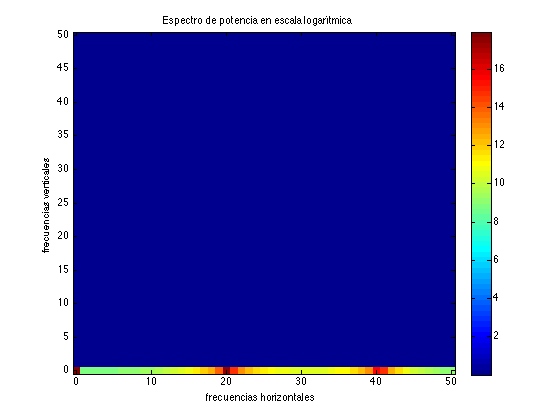
- En la tercera figura, dibujamos \(\log(1+P)\) para visualizar mejor los valores. Vemos que también \((0,40)\) es un máximo relativo del espectro de potencia. Este máximo corresponde a lo que se llama el primer armónico \( (2*20)\) de la frecuencia fundamental \((20)\).
- Finalmente, observar que, como en el caso 1D, por simetría, sólo necesitamos dibujar la mitad de los rangos de frecuencia, tanto en horizontal como en vertical.
f=imread('lines.tif'); % f es de tipo entero f=double(f); % lo pasamos a doble precisión [M,N]=size(f); figure,imagesc(f),colormap(gray) F=fft2(f)/sqrt(M*N); % calculamos la transformada de Fourier % fijarse en la normalización cF=fftshift(F); % centramos en el origen cP=abs(cF).^2; % calculamos el espectro de potencia (centrado) Mrange=0:floor(M/2); % rangos de representación Nrange=0:floor(N/2); figure,imagesc(Mrange,Nrange,cP(floor(M/2)+1:M,floor(N/2)+1:N)), axis xy, title('Espectro de potencia'), xlabel('frecuencias horizontales'), ylabel('frecuencias verticales'),colorbar figure,imagesc(Mrange,Nrange,log(1+cP(floor(M/2)+1:M,floor(N/2)+1:N))), axis xy, title('Espectro de potencia en escala logarítmica'), xlabel('frecuencias horizontales'), ylabel('frecuencias verticales'),colorbar
Fijarse que dividimos por \(\sqrt{MN}\) para normalizar la energía. De esta manera \(\left\|f\right\|=\left\|F\right\|\):
out1=norm(F); out2=norm(double(f)); % la función norm no existe para uint8 fprintf('out1=%d out2= %d\n',out1,out2)
out1=1.283468e+04 out2= 1.283468e+04
La normalización de la transformada inversa de Fourier (ifft2) se consigue multiplicando por \(\sqrt{MN}\)
f2=ifft2(F)*sqrt(M*N); f2=real(f2); % truncamos los valores complejos (muy pequeños) % y así quitamos errores out3=norm(f2); fprintf('out3=%d ',out3)
out3=1.283468e+04
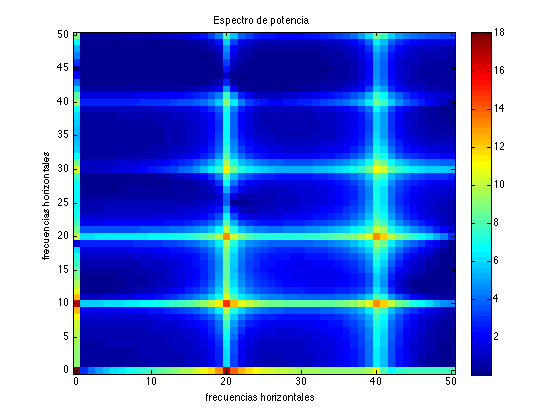
Ejemplo 4. Ahora cargamos una imagen periódica en las dos direcciones dots.tif y dibujamos la imagen y \(\log(1+P)\). En este caso, el máximo corresponde a las frecuencias \((20,10)\). Los correspondientes armónicos se pueden visualizar también como máximos relativos.
f=imread('dots.tif'); % f es tipo entero f=double(f); % hacemos los cálculos en doble precisión [M,N]=size(f); figure,imagesc(f),colormap(gray) F=fft2(f)/sqrt(M*N); % aplicamos la transformada de Fourier % fijarse en la normalización cF=fftshift(F); % centramos en el origen cP=abs(cF).^2; % calculamos el espectro de potencias (centrado) Mrange=0:floor(M/2); % rangos de representación Nrange=0:floor(N/2); figure,imagesc(Mrange,Nrange,log(1+cP(floor(M/2)+1:M,floor(N/2)+1:N))), axis xy title('Espectro de potencia'), xlabel('frecuencias horizontales'), ylabel('frecuencias horizontales'),colorbar

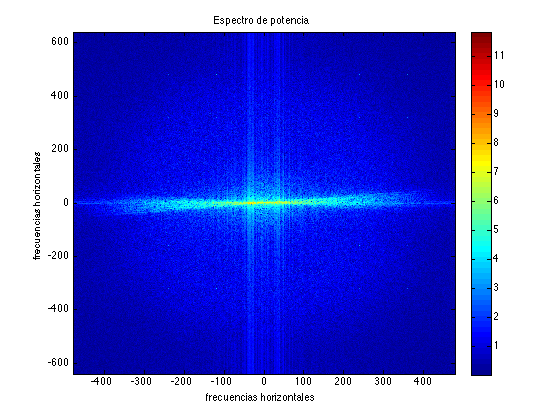
Ejemplo 5. Finalmente hacemos una prueba con una imagen real canes.jpg que tiene una frecuencia horizontal perceptible, como se puede observar por el alineamiento de los máximos relativos con el eje horizontal de \(\log(1+P)\). En este caso, hemos dibujado el rango de frecuencias completo para una mejor visualización del eje horizontal \(X=0\). Observar la simetría respecto a ambos ejes.
f=imread('canes.jpg'); f=rgb2gray(f); f=double(f); [M,N]=size(f); figure,imagesc(f),colormap(gray) F=fft2(f)/sqrt(M*N); cF=fftshift(F); aF=abs(cF); figure,imagesc(-floor(M/2):floor(M/2),-floor(N/2):floor(N/2),log(1+aF)), axis xy % dibujamos el rango completo title('Espectro de potencia'), xlabel('frecuencias horizontales'), ylabel('frecuencias horizontales'),colorbar

Método del valor umbral (Thresholding)
Podemos recuperara una imagen a partir del conjunto de coeficientes \(F\) usando la Transformada Inversa de Fourier (función Matlab ifft2). Como hemos visto, en general, no todos los coeficientes tienen el mismo valor. Para usar solo los más importantes, podemos selecionar aquellos que son mayores en módulo que un umbral (threshold) dado \(T\). Es decir, hacemos cero todos los coeficientes contenidos en el conjunto: \[ S_T=\left\{0\leq m\leq M-1, 0\leq n \leq N-1 : \left| F(m,n)\right| \geq T\right\} .\]
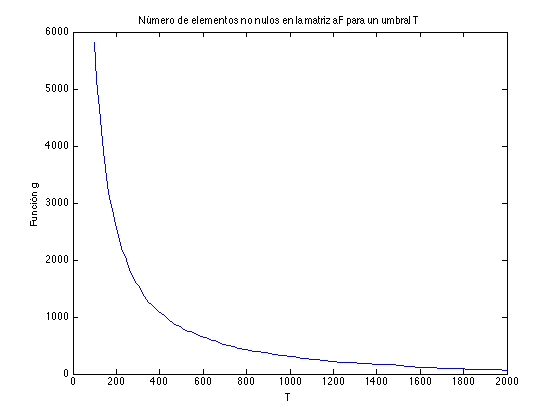
Sea \(g(T)\) el número de índices en \(S_T\). Por un lado, para \(T=0\) tenemos \(g(0)= MN\), porque \(\left| F(m,n)\right| \) es siempre no negativo. Por otra parte para \(T> \max \left| F(m,n)\right| \) tenemos \(g(T)=0\). Tener en cuenta que \(g\) es una función decreciente que depende de \(T\). Dibujamos \(g\) usando la orden nnz, que da el número de elementos distintos de cero de una matriz.
aF=abs(F); g=@(T) nnz(aF >=T); g_vector=[]; for T=100:10:2000 g_vector=[g_vector g(T)]; end plot(100:10:2000,g_vector), ylabel('Función g'), xlabel('T') title('Número de elementos no nulos en la matriz aF para un umbral T')
Ahora aplicamos un umbral, por ejemplo, hagamos cero todos los coeficientes que son más pequeños que un cierto \(T\). ¿Cómo escogemos \(T\)? Para empezar,
- \(T\) debe ser lo bastante grande para despreciar algún coeficiente.
- \(T\) debe ser lo bastante pequeño para conservar algún coeficiente.
Cojamos, por ejemplo, \(T=100\) y veamos el resultado:
T=100; c=F.*(abs(F)>=T); fM=real(ifft2(c))*sqrt(M*N); imagesc(fM),colormap(gray)

Vamos a convertir la matriz double en una matriz con el formato inicial (gray)
f_im=fM*255/max(max(fM)); % Reescalamos los valores a [0 255] f_sal=uint8(f_im); % Transformamos en enteros sin signo de 8 bits imwrite(f_sal,'canes_bn_comprimida.jpg') % Guardamos como jpg
Finalmente, calculamos la razón entre el número de coeficientes no nulos de la transformada de Fourier, \(F\), y los de la matriz a la que le hemos aplicado el umbral \(c\):
out1=nnz(F); % para recuperar la imagen de partida out2=nnz(c); % para recuperar la imagen a la que se ha aplicado el umbral out3=out1/out2; % razón de compresión fprintf('out1=%d out2=%d out3=%.0f\n',out1,out2,out3)
out1=1228800 out2=5823 out3=211
Ejercicio
Dada una imagen dada de talla \(M\times N\), queremos comprimirla de acuerdo con una determinada razón \(r\) manteniendo los coeficientes de Fourier más significativos. Es decir, queremos determinar el umbral, \(T\), tal que la razón de compresión sea igual a \(r\). O lo que es lo mismo, queremos calcular \(T\) de forma que \( \frac{g(T)}{MN}=r \). Para hacer esto, calculamos la raíz de la función \[h(T)=g(T) -rMN\]
Seguir los pasos siguientes para escribir el programa compresion.m:
- Cargar la imagen cameraman.tif y definir \(r=1/200\).
- Calcular su tranformada de Fourier, \(F\), y también el máximo y el mínimo de su módulo \(maxF\) y \(minF\).
- La función \( h(T) \) se calcula usando nnz(aF>T), con aF=abs(F). Para hacerse una idea, dibujar esta función en el itervalo T=MinF:200.
- Como \(h(T)\) es decreciente, podemos buscar para qué \(T\) hay un cambio en el signo de \(h\) y por lo tanto una aproximación de la raíz de \(h\). Comprobar el signo de \(h\) desde \(T=minF\) hasta \(T=maxF\).
- Una vez hemos determinado el valor aproximado de \(T\) para el que cambia de signo \(h\), podemos definir la matriz de coeficientes de Fourier con el umbral aplicado y la imagen comprimida como hicimos en el Ejemplo 3. Dibuja las imágenes original y comprimida. ¿Qué observas cuando comparas los resultados con los del Ejemplo 3?
- Comprueba que la razón de compresión está próxima a \(r\), como hicimos al final del Ejemplo 3.
- Adapta uno de los programas biseccion.m que hiciste en la Práctica de Raíces de Ecuaciones no lineales para calcular un valor aproximado de la única raíz de \(h\). ¿Por qué la raíz es única? Comprueba que la raíz es parecida a la obtenida en el apartado anterior.
- Transforma el programa en una función con argumentos de entrada una imagen y una razón \(r\) y con argumentos de salida el umbral \(T\) y el dibujo de las imágenes originales y comprimidas.