Derivación numérica
Contenidos
Derivada primera de funciones de una variable
Buscamos obtener una aproximación de \(f'\) en un punto \(\hat x\) en función de valores de \(f\) en un número finito de puntos cercanos a \(\hat x\).
¿Por qué?
- Porque sólo conocemos los valores de \(f\) en un número finito de puntos \(x\).
- Porque es menos costoso calcular la aproximación que el valor exacto.
A partir de la definición de derivada \[ f'(\hat x)=\lim_{h\to0}\frac{f(\hat x+h)-f(\hat x)}{h} \]
podemos obtener tres aproximaciones o fórmulas en diferencias finitas
Diferencias finitas progresivas \[ (\delta^+ f)(\hat x)=\frac{f(\hat x+h)-f(\hat x)}{h}\] Diferencias finitas regresivas \[ (\delta^- f)(\hat x)=\frac{f(\hat x)-f(\hat x -h)}{h}\] Diferencias finitas centradas \[ (\delta f)(\hat x)=\frac{1}{2}\big((\delta^+ f)(\hat x)+(\delta^- f)(\hat x)\big)= \frac{f(\hat x+h)-f(\hat x-h)}{2h}\]
Tener en cuenta que si solo usamos una de estas fórmulas no podemos calcular la derivada al menos en un extremo del intervalo. Por ejemplo, si usamos la fórmula progresiva no podemos calcular \((\delta^+ f)(b)\) porque necesitamos \(f(b+h)\) que, en general, es desconocido.
Órdenes Matlab Matlab es más eficiente cuando usa vectorización. Para los ejecicios propuestos es útil la orden diff(X) que calcula \((X_2-X_1, X_3-X_2,\ldots,X_n-X_{n-1})\), y la orden norm(X) que calcula la norma euclídea de un vector \(X\), por ejemplo \[ \text{norm}(X)=\sqrt{\sum_{i=1}^n X_i^2}\]
Ejercicio 1 Dada la función \(f(x)=e^x\) en \([h,1-h]\) y para h=0.01 y h=0.001:
- Calcular y dibujar su derivada exacta.
- Calcular y dibujar, sobre la figura anterior, su derivada aproximada usando diferencias finitas progresivas, \(df_p\), regresivas, \(df_r\), y centradas, \(df_c\).
- Calcular y dibujar, en una figura nueva, el error en cada punto para cada una de las aproximaciones, \(f'(x_i)-df_a(x_i)\), donde \(x_i\) son los puntos y \(a=p,~r\) o \(c\).
- Calcular el error global relativo de cada aproximación \[ Error_{Global\,rel}=\sqrt{\frac{\sum_{i=1}^n (f'(x_i)-df_a(x_i))^2}{\sum_{i=1}^n (f'(x_i))^2}}.\]
Ejercicio1
h E(df_p) E(df_r) E(df_c) 0.010 5.016708e-03 4.983375e-03 1.666675e-05 h E(df_p) E(df_r) E(df_c) 0.001 5.001667e-04 4.998334e-04 1.666667e-07
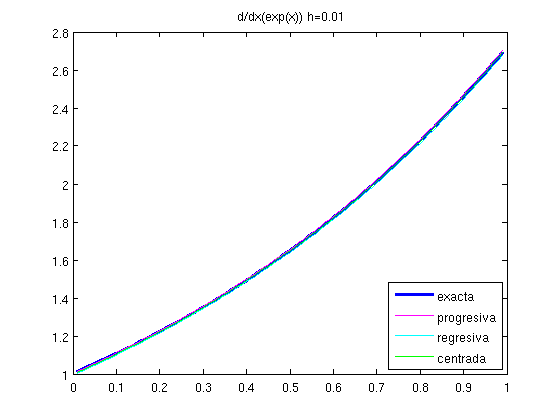
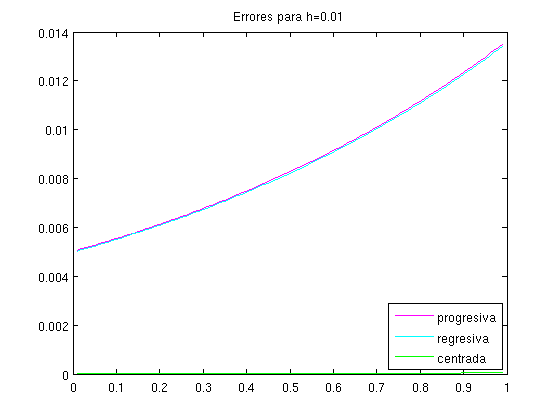
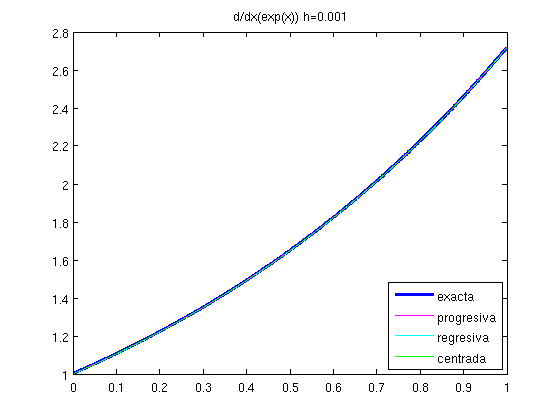
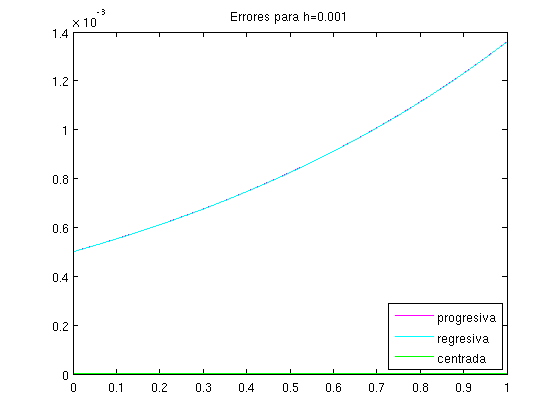
Vemos que la fórmula centrada da lugar a un error menor. Esto se debe a que las fórmulas progresiva y regresiva son de orden 1 y la fórmula centrada es de orden 2.
¿Es posible conseguir aproximaciones de orden 2 para \(f'(a)\) y \(f'(b)\)?
Si usamos un polinomio de interpolación de Lagrange \(f\) de \(2^o\) grado en \(x_1\), \(x_2\), \(x_3\), siendo \(y_j=f(x_j)\).
\[ p(x)=[y_1]+[y_1,y_2](x-x_1)+[y_1,y_2,y_3](x-x_1)(x-x_2)\]
Tenemos \[[y_1]=y_1,\quad [y_1,y_2]=\frac{y_1-y_2}{x_1-x_2}=\frac{y_2-y_1}{h}, \quad [y_1,y_2,y_3]=\frac{[y_1,y_2]-[y_2,y_3]}{x_1-x_3}=\frac{1}{2h}(\frac{y_1-y_2}{h} -\frac{y_2-y_3}{h}\big)= \frac{1}{2h^2}(y_1-2y_2+y_3)\]
Es decir \[[y_1]=y_1,\quad [y_1,y_2]=\frac{y_2-y_1}{h},\quad [y_1,y_2,y_3]= \frac{1}{2h^2}(y_1-2y_2+y_3)\]
Y el polinomio interpolante es \[ p(x)=y_1+\frac{y_2-y_1}{h} (x-x_1)+ \frac{1}{2h^2}(y_1-2y_2+y_3)(x-x_1)(x-x_2) \]
Y su derivada \[ p'(x)=\frac{y_2-y_1}{h}+ \frac{1}{2h^2}(y_1-2y_2+y_3)((x-x_1)+(x-x_2)) \]
Sustituyendo \(x\) por \(x_1\) obtenemos una fórmula progresiva de orden 2 \[ f'(x_1)\approx p'(x_1)=\frac{1}{2h}(-3f(x_1)+4f(x_2)-f(x_3))\]
sustituyendo \(x\) por \(x_2\), la fórmula centrada que ya teníamos \[ f'(x_2)\approx p'(x_2)= \frac{1}{2h}(f(x_3)-f(x_1))\]
y sustituyendo \(x\) por \(x_3\) obtenemos una fórmula regresiva de orden 2 \[ f'(x_3)\approx p'(x_3)=\frac{1}{2h}(f(x_1)-4f(x_2)+3f(x_3))\]
Que también podemos escribir de la forma: \[ \begin{array}{ll} f'(\hat x)\approx \frac{1}{2h}(-3f(\hat x)+4f(\hat x+h)-f(\hat x+2h)) & \mathbf{Progresiva}\\ f'(\hat x)\approx \frac{1}{2h}(f(\hat x+h)-f(\hat x-h)) & \mathbf{Centrada}\\ f'(\hat x)\approx \frac{1}{2h}(f(\hat x-2h)-4f(\hat x-h)+3f(\hat x)) & \mathbf{Regresiva} \end{array} \]
Ejercicio 2 Dada la función \(f(x)=\frac{1}{x}\) en \([0.2,1.2]\), y \(h=0.01\).
- Calcular su derivada aproximada utilizando la fórmula centrada para sus puntos interiores y progresiva y regresiva de orden 1 (dos puntos) para \(f'(0.2)\) y \(f'(1.2)\) respectivamente.
- Calcular su derivada aproximada utilizando la fórmula centrada para sus puntos interiores y progresiva y regresiva de orden 2 (tres puntos) para \(f'(0.2)\) y \(f'(1.2)\) respectivamente.
- Calcular la derivada exacta en \([0.2,1.2]\) y el error global relativo para las dos aproximaciones.
Ejercicio2
h E(df_1) E(df_2) 0.010 1.786397e-02 2.171714e-03
Derivada segunda de funciones de una variable
A partir del polinomio de interpolación. \[ p(x)=[y_1]+[y_1,y_2](x-x_1)+[y_1,y_2,y_3](x-x_1)(x-x_2) \] Derivando dos veces el polinomio anterior obtenemos \[p''(x_2)=2[y_1,y_2,y_3]= \frac{1}{h^2}(y_1-2y_2+y_3)\quad (1)\]
Ejercicio 3 Dada la función \(f(x)=\sin(2\pi x)\) en \([0,1]\) y \(h=0.01\):
Calcular su derivada segunda exacta en \([0,1]\) y su derivada segunda aproximada utilizando la fórmula (1) y el error relativo de la aproximación en el intervalo \([h,1-h]\). Puedes usar la orden Matlab diff(X,2).
Ejercicio3
h Error 0.010 3.289435e-04
Derivadas de funciones de dos variables
Sea \(\Omega =[a,b]\times[c,d]\subset \mathbb{R}^2\). Introducimos particiones uniformes \begin{eqnarray*} a=x_1<x_2<\ldots<x_{M-1}<x_M=b \\ c=y_1<y_2<\ldots<y_{N-1}<y_N=d \end{eqnarray*} Si llamamos a un punto \((x_m,y_n)\) sus vecinos son
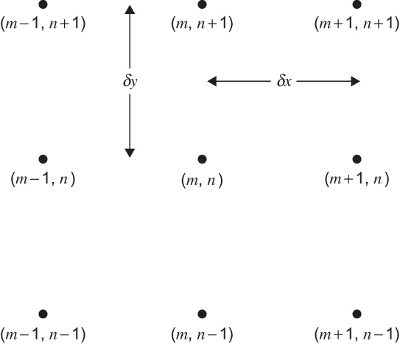
Podemos construir las fórmulas de forma análoga a como hicimos con las fórmulas para una variable. Por ejemplo
- Derivada parcial (progresiva): \(\partial_x f(x_m,y_n)\) \[ (\delta_x^+f)(x_m,y_n)= \frac{f(x_{m+1},y_n)-f(x_{m},y_n)}{h_x} \]
- Gradiente (centrado): \(\nabla f(x_m,y_n)=(\partial_x f(x_m,y_n),\partial_y f(x_m,y_n))\) \[ (\frac{f(x_{m+1},y_n)-f(x_{m-1},y_n)}{2h_x}, \frac{f(x_{m},y_{n+1})-f(x_{m},y_{n-1})}{2h_y})\quad (2)\]
- Divergencia (centrada): \(\mathrm{div} (\mathbb{f}(x_m,y_n))=\partial_x f_1(x_m,y_n)+\partial_y f_2(x_m,y_n)\) \[ \frac{f_1(x_{m+1},y_n)-f_1(x_{m-1},y_n)}{2h_x}+ \frac{f_2(x_{m},y_{n+1})-f_2(x_{m},y_{n-1})}{2h_y} \quad (3) \]
- Laplaciana (centrada): \(\Delta f(x_m,y_n)=\partial_{xx} f(x_m,y_n)+ \partial_{yy} f(x_m,y_n)\) \[ \frac{f(x_{m+1},y_n)-2f(x_m,y_n)+f(x_{m-1},y_n)}{h_x^2}+ \frac{f(x_{m},y_{n+1})-2f(x_m,y_n)+f(x_{m},y_{n-1})}{h_y^2} \quad (4) \]
Pero antes de usar estas fórmulas, recordemos como se representan las funciones de dos variables, tanto escalares como vectoriales, en Matlab.
Matlab representa las funciones de dos variables en coordenadas cartesianas en dominios rectangulares. Como en el caso de las funciones de una variable nosotros decidimos el número de puntos que utilizaremos en la representación.
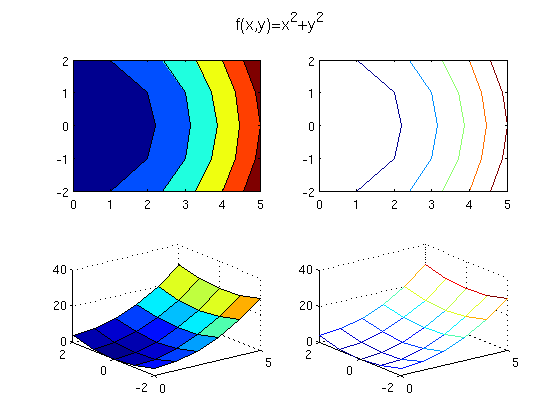
Si queremos representar la función escalar \(f(x,y)=x^2+y^2\) en \(x \in [0,5]\) con paso \(h_x=1\) e \(y \in [-2,2]\) con paso \(h_y=1\)
[x,y]=meshgrid(0:1:5,-2:1:2)
x =
0 1 2 3 4 5
0 1 2 3 4 5
0 1 2 3 4 5
0 1 2 3 4 5
0 1 2 3 4 5
y =
-2 -2 -2 -2 -2 -2
-1 -1 -1 -1 -1 -1
0 0 0 0 0 0
1 1 1 1 1 1
2 2 2 2 2 2
y hemos creado dos matrices. Calculamos ahora los valores de \(z=f(x,y)=x^2+y^2\) para cada par de \((x_{ij},y_{ij}) \quad i=1,\ldots,m,\,j=1,\ldots,n\) siendo \(m\) y \(n\) el número de filas y columnas tanto de x como de y. Operando elemento a elemento obtenemos una matriz z de dimensiones \(m\times n\)
z = x.^2+y.^2
z =
4 5 8 13 20 29
1 2 5 10 17 26
0 1 4 9 16 25
1 2 5 10 17 26
4 5 8 13 20 29
Con estas tres matrices x, y, z ya podemos representar la función \(f\). Las funciones contour y surf son las más usadas.
figure
subplot(2,2,1), contourf(x,y,z)
subplot(2,2,2), contour(x,y,z)
subplot(2,2,3), surf(x,y,z)
subplot(2,2,4), mesh(x,y,z)
suptitle('f(x,y)=x^2+y^2')
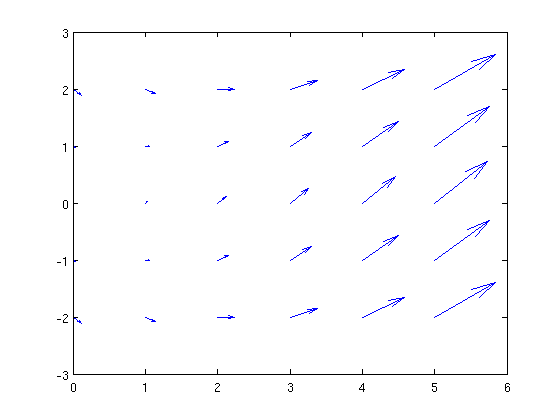
Si queremos representar una función vectorial podemos usar, junto con meshgrid, el comando quiver.
u1=x.^2+y.^2; u2=x.^2-y.^2; figure quiver(x,y,u1,u2)
Ejercicio 4 Calcular el gradiente de una función usando la orden Matlab gradient: [fx,fy] = gradient(f,hx,hy) que devuelve el gradiente (calculado numéricamente) de la función f, usando los pasos hx y hy.
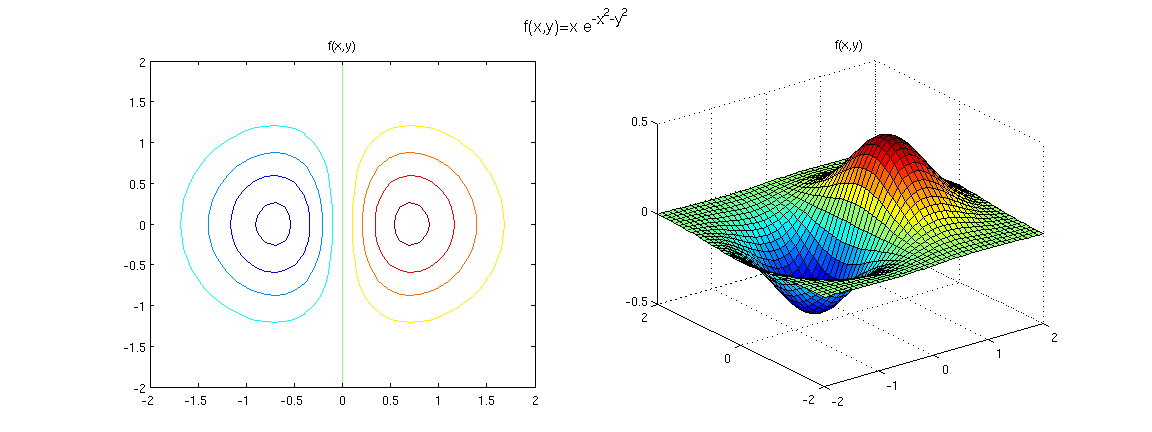
- Dibujar, usando contour y surf la función \(f(x,y)=x e^{-x^2-y^2}\) en \([-2,2]\times[-2,2]\) con \(h_x=h_y=0.1\).
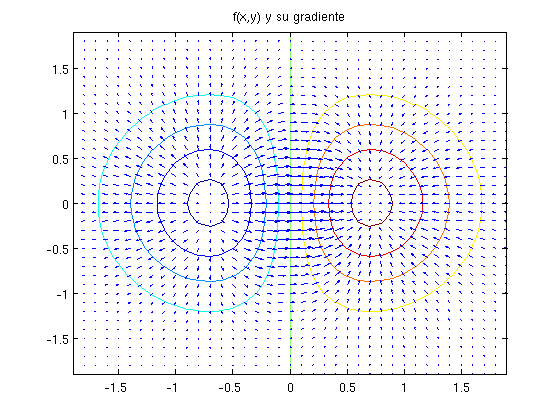
- Calcular, usando la función de Matlab gradient, el gradiente de \(f\) y dibujarlo en la misma figura con la función \(f\).
- Calcular el error global relativo de la aproximación usando norm.
Ejercicio4
Error relativo 1.435691e-02
Ejercicio 5 Calcular la divergencia de una función usando la orden Matlab divergence: div = divergence(x,y,f1,f2) que devuelve la divergencia (calculada numéricamente) del campo vectorial \(\mathbb{f}=(f_1(x,y),f_2(x,y))\). Las matrices \(x\) e \(y\) nos dan las coordenadas para \((f_1,f_2)\) y se generan con meshgrid.
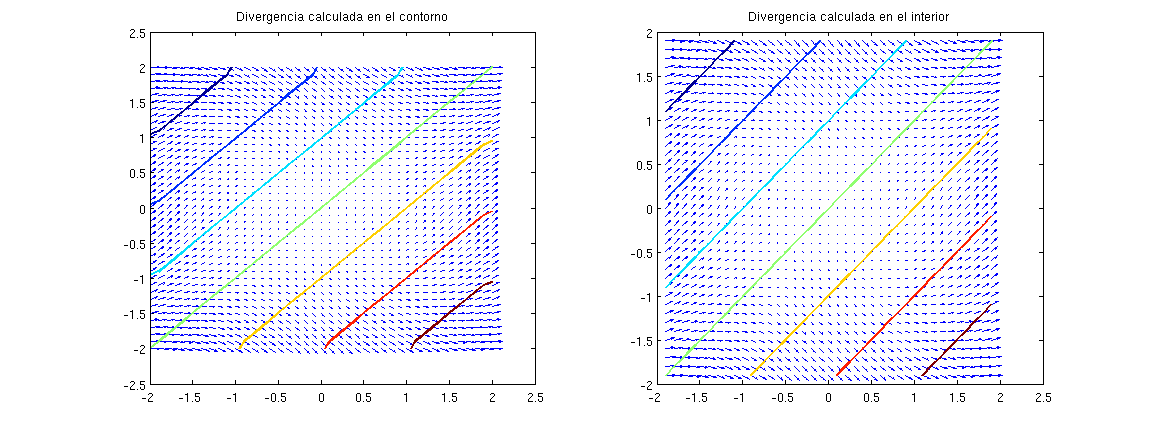
- Calcular, usando la orden Matlab divergence, la divergencia de \(\mathbb{f}(x,y)=(x^2+y^2,x^2-y^2)\) en \([-2,2]\times[-2,2]\) con \(h_x=h_y=0.1\). Dibujar en la misma figura \(\mathbb{f}\) con quiver y \(\text{div} (\mathbb{f})\) usando contour.
- Se aprecia un efecto en los bordes debido a una mala aproximación de la divergencia en estos puntos. Rehacer los dibujos restringiendo la representación de la divergencia a \([-2+h_x,2-h_x]\times[-2+h_y,2-h_y]\).
- Calcular el error global relativo en ambos casos usando norm.
Ejercicio5
Error 1 Error 2 9.333167e-03 2.698803e-16
Ejercicio 6 Calcular la laplaciana de una función usando la orden Matlab del2: L = del2(f,h_x,h_y). Cuando f es una matriz, L es una aproximación discreta de \(\frac{1}{4} (\partial_{xx} f(x,y)+\partial_{yy} f(x,y))\). La matriz L es del mismo tamaño que f, siendo cada elemento igual a la diferencia entre un elemento de f y el promedio entre sus cuatro vecinos.
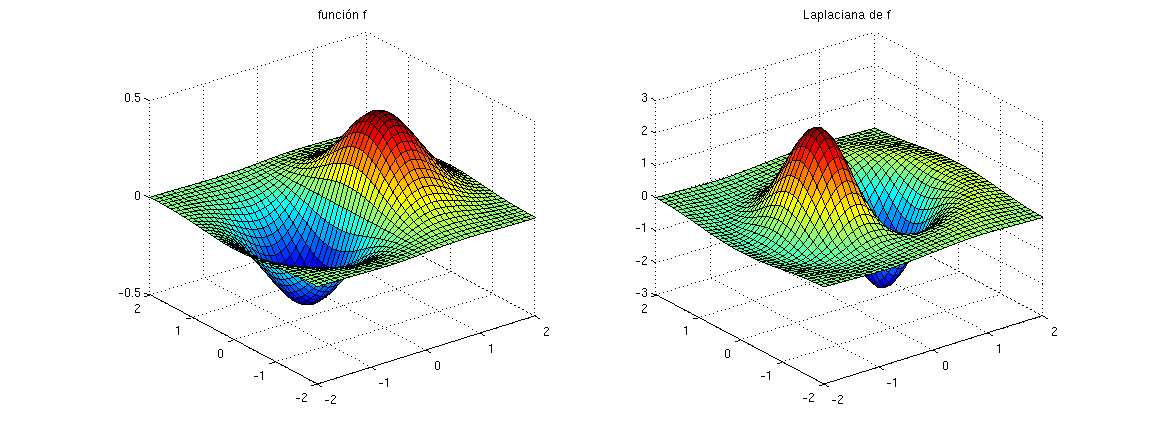
- Calcular, usando la orden Matlab del2, la laplaciana de \(f(x,y)=x e^{-x^2-y^2}\) en \([-2,2]\times[-2,2]\) con \(h_x=h_y=0.1\). Dibuja la función y su Laplaciana usando surf.
- Calcular la solución exacta y el error global relativo usando norm.
Ejercicio6
Error relativo 5.914553e-03