Convolución

Contenidos

El problema del borde
Convolución en dos dimensiones. Filtrado de imágenes

La convolución es una aplicación importante de la integración. Es una operación en la que:

Para un kernel dado \(g:\mathbb{R}^n\to\mathbb{R}\), y
Para una función de entrada \(f:\mathbb{R}^n\to\mathbb{R}\)
La operación da una función de salida \(f*g:\mathbb{R}^n\to\mathbb{R}\), que es \[f*g(x)=\int_{\mathbb{R}^n} g(x-y)f(y) dy.\]

La versión discreta usa integración numérica. En el caso unidimensional, tenemos \[f*g(x_i)=h \sum_{j=-\infty}^\infty g(x_i-x_j)f(x_j) \] donde \(\{x_j\}\) es una malla uniforme en \(\mathbb{R}\) con paso \(h\).

El problema del borde

Si realizamos una convolución en un intervalo cerrado, aparece el problema del borde. Para las \(x\) que están cerca de la frontera, el producto \(g(x_i-x_j)f(x_j)\) no está definido, porque no podemos utilizar \(x_j\) fuera de la frontera. Existen varias estrategias para corregir esta situación. A continuación, vamos a ver un ejemplo de aplicación de la convolución a la derivación numérica.

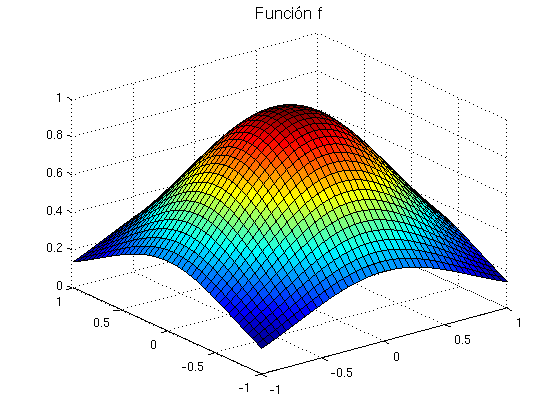
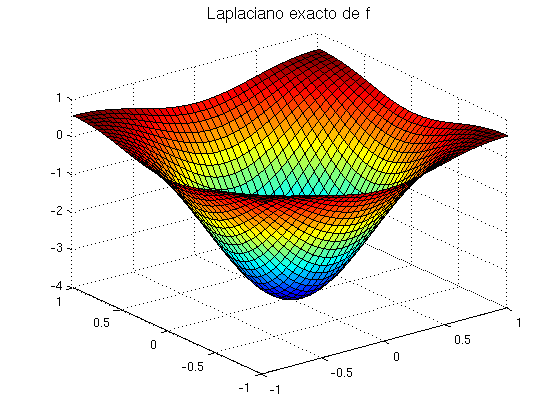
Empezamos definiendo la función y su Laplaciano exacto en el cuadrado \( [-1,1]\times [-1,1]\). El Laplaciano es \[\Delta f(x,y)=\frac{\partial^2 f(x,y)}{\partial x^2}+ \frac{\partial^2 f(x,y)}{\partial y^2}\]

f=@(x,y) exp(-(x.^2+y.^2));
Lf=@(x,y) 4*f(x,y).*(x.^2+y.^2-1); % Laplaciano de f

h=0.05;% paso de la malla (para los ejes x e y)
[x,y]=meshgrid(-1:h:1);
[s1,s2]=size(x);

F=f(x,y);
Le=Lf(x,y); % Laplaciano exacto discretizado

figure
surf(x,y,F)
title('Función f','FontSize',14)
figure
surf(x,y,Le)
title('Laplaciano exacto de f','FontSize',14)

Ahora definimos el Laplaciano usando convolución con el kernel Laplaciano.

Como el Laplaciano es \[\Delta f(x_m,y_n)=\frac{\partial^2 f(x_m,y_n)}{\partial x^2}+ \frac{\partial^2 f(x_m,y_n)}{\partial y^2}\]

Y su forma discreta, con el mismo paso para \(x\) e \(y\) es

\[ \frac{f(x_{m+1},y_n)-2f(x_m,y_n)+f(x_{m-1},y_n)}{h^2}+ \frac{f(x_{m},y_{n+1})-2f(x_m,y_n)+f(x_{m},y_{n-1})}{h^2} \]

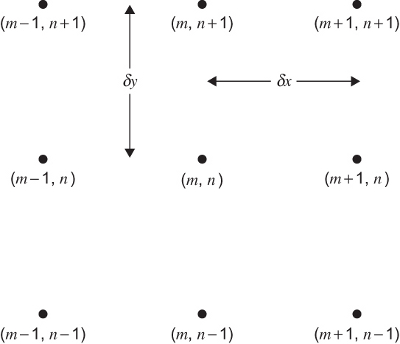
El kernel para calcular el Laplaciano es \[ K= \dfrac{1}{h^{2}}\begin{pmatrix}\begin{array}{crc} 0 & 1 & 0\\ 1 & -4 & 1\\ 0 & 1 & 0 \end{array}\end{pmatrix} \]

Por lo tanto, si \(\Delta f=0\) en un punto, significa que, en ese punto, \(f\) es igual a su promedio en los puntos cercanos. Y podemos decir que el Laplaciano es un operador que promedia. Más exactamente, es una diferencia de promedios.

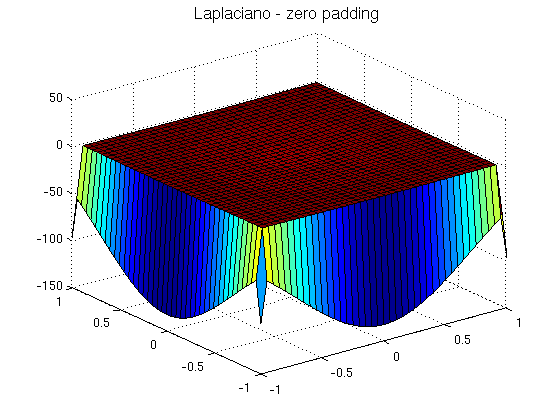
El primer metodo para intentar resolver el problema del borde es zero-padding, que extiende \(f\) en el borde dándole valor cero fuera del dominio. Se usa la orden de Matlab conv2 para calcular la convolución bidimensional de las dos matrices.

K=(1/h^2)*[0 1 0; 1 -4 1; 0 1 0]; % kernel para calcular el Laplaciano
FA=[         zeros(1,s2+2)         ;
    zeros(s1,1)    F    zeros(s1,1);
             zeros(1,s2+2)         ];
Lz=conv2(FA,K,'valid');% esta opción da la región sin el borde añadido para el padding
figure
surf(x,y,Lz)
title('Laplaciano - zero padding','FontSize',14)
figure
surf(x(2:end-1,2:end-1),y(2:end-1,2:end-1),Lz(2:end-1,2:end-1))
title('Laplaciano - zero padding (sin borde)','FontSize',14)
Error_relativo=norm(Lz-Le)/norm(Le)

Error_relativo =
   15.4850

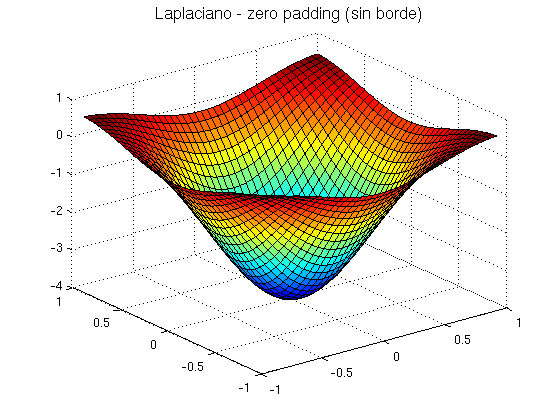
Otra posibilidad es extender la región por simetría

FA=[  0    F(1,:)         0   ;
    F(:,1)    F       F(:,end);
      0    F(end,:)       0    ];
Ls=conv2(FA,K,'valid');
figure
surf(x,y,Ls)
title('Laplaciano - simetría','FontSize',14)
figure
surf(x(2:end-1,2:end-1),y(2:end-1,2:end-1),Ls(2:end-1,2:end-1))
title('Laplaciano - simetría (sin borde)','FontSize',14)
Error_relativo=norm(Ls-Le)/norm(Le)

Error_relativo =
    1.6716

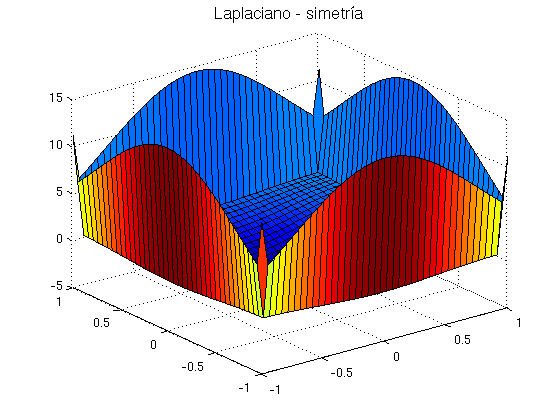
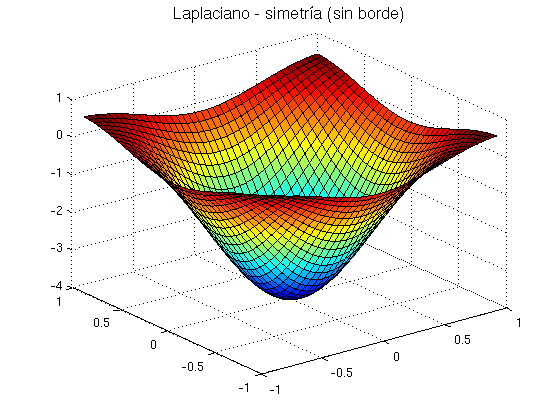
Como en este ejemplo en particular, conocemos la función exacta fuera del recinto, vamos a hacer la extensión por extrapolación. En general esto no se puede hacer porque no conocemos los valores de la función fuera del dominio. La extrapolación de debe hacer usando otro método.

[x1,y1]=meshgrid(-1-h:h:1+h);
FA=f(x1,y1);
Lx=conv2(FA,K,'valid');
figure
surf(x,y,Lx)
title('Laplaciano - falsa extrapolación','FontSize',14)
Error_relativo=norm(Lx-Le)/norm(Le)

Error_relativo =
    0.0010

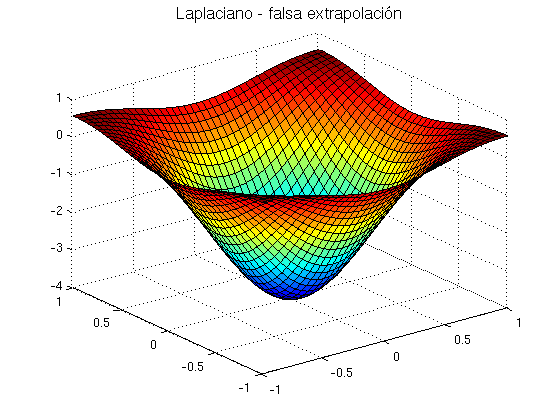
Por último, vamos a usar la orden de Matlab del2 para calcular el Laplaciano. Esta orden usa una regla de extrapolación que utiliza únicamente valores interiores al dominio.

Lm=4*del2(F,h);
figure
surf(x,y,Lm)
title('Laplaciano - extrapolation verdadera','FontSize',14)
Error_relativo=norm(Lm-Le)/norm(Le)

Error_relativo =
    0.0024

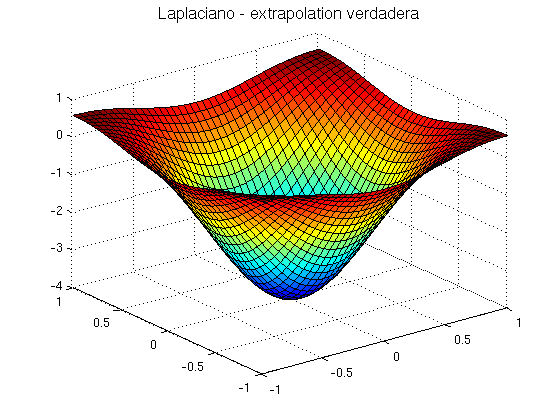
Ejercicio 1. Vamos a corregir el problema del borde usando una aproximación de la derivada segunad de orden dos. Definir la función unidimensional \(f(x)=\exp(-x^2)\) y su Laplaciano (derivada segunda). La fórmula para la derivada segunda discreta es \[f''(\hat x) \approx \frac{1}{h^2}(f(\hat x-h)-2f(\hat x)+f(\hat x+h)),\] y el kernel de convolución correspondiente es \(K=(1/h^2)*[1,-2,1]\), y el dominio \( [-1,1]\) estará discretizado con una malla uniforme de paso \(h=0.05\).

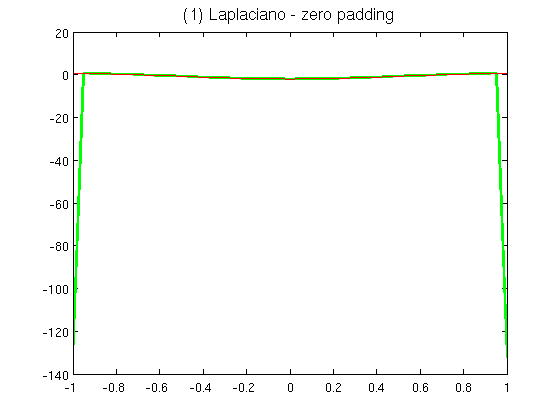
Realizar la convolución que calcula el Laplaciano con zero-padding y dibujarlo junto con el Laplaciano exacto. Observar el problema del borde.
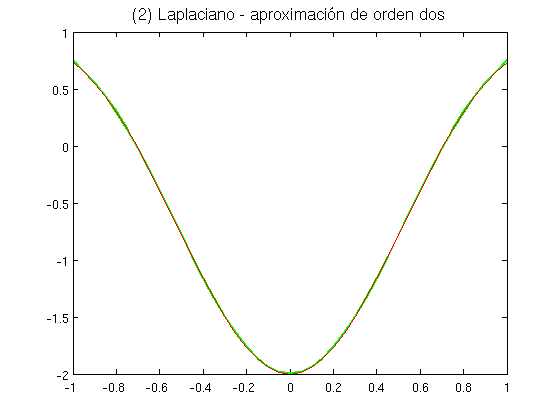
Modificar la aproximación del Laplaciano en el borde sustituyéndo el primer y el último elemento por las aproximaciones progresiva y regresiva de segundo orden del Laplaciano dadas por las fórmulas \[ f''(\hat x)\approx \frac{1}{h^2} (2f(\hat x)-5f(\hat x+h)+4f(\hat x+2h)-f(\hat x+3h))\\ f''(\hat x)\approx \frac{1}{h^2} (2f(\hat x)-5f(\hat x-h)+4f(\hat x-2h)-f(\hat x-3h))\] Dibujar esta aproximación junto con el Laplaciano exacto y calcular el error relativo.
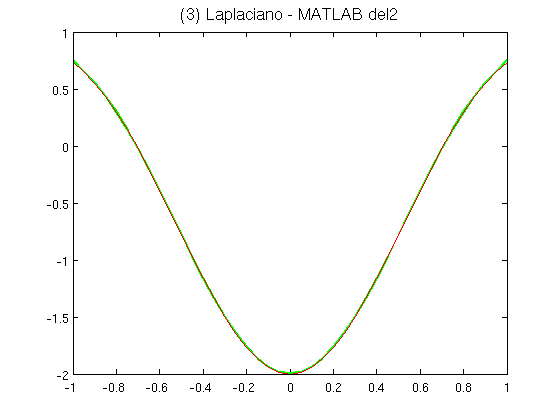
Usar la orden del2 para obtener la aproximación discreta del Laplaciano. Dibujar esta aproximación junto con el Laplaciano exacto y calcular el error relativo.

Ejercicio1

Error_relativo_1 =
   25.0786
Error_relativo_2 =
    0.0034
Error_relativo_3 =
    0.0034

Convolución en dos dimensiones. Filtrado de imágenes

Existen muchas tareas en el procesado de imágenes que se realizan mediante convolución con un kernel adecuado. Ver, por ejemplo, Gimp.

Paso 1. Leemos la imagen y añadimos ruido gaussiano.

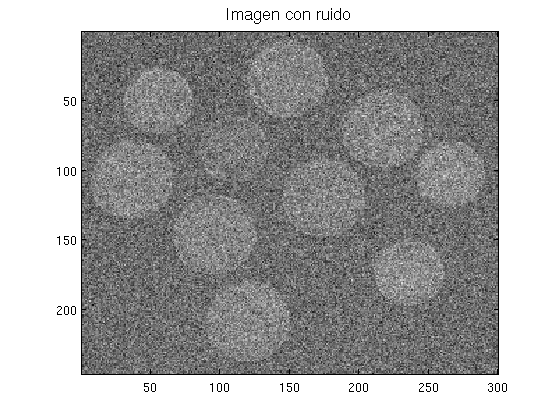
% Imagen
I0=imread('moon.tif');
I0=im2double(I0);
figure
imagesc(I0),axis image,colormap('gray')
title('Imagen','FontSize',14)

% Imagen con ruido
ruido=0.1;
I=I0+ruido*randn(size(I0));
figure
imagesc(I),axis image,colormap('gray')
title('Imagen con ruido','FontSize',14)

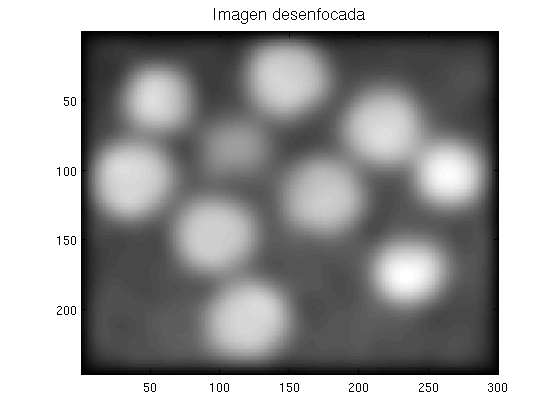
Paso 2. Realizamos la convolución de forma iterativa con un kernel de desenfoque (o suavizado). \[ kS= \dfrac{1}{9}\begin{pmatrix}\begin{array}{ccc} 1 & 1 & 1\\ 1 & 1 & 1\\ 1 & 1 & 1 \end{array}\end{pmatrix} \]

n=3;
kS=ones(n,n)/n^2; % kernel de desenfoque de orden n
I1=I;
for k=1:100
    I2=conv2(I1,kS,'same');
    I1=I2;
end
figure
imagesc(I2),axis image,colormap('gray')
title('Imagen desenfocada','FontSize',14)

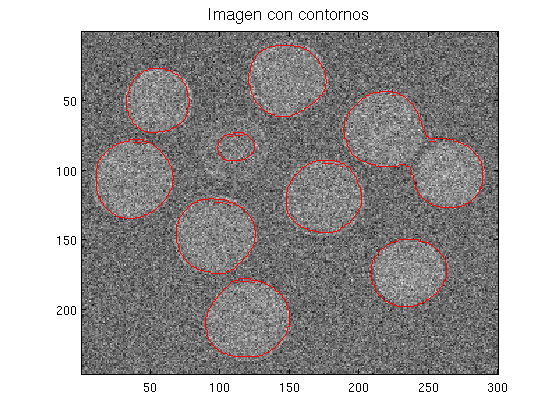
Paso 3. Usamos el kernel Laplaciano para encontrar los contornos. Descargar la función dibuja_contornos.m.

kL=[0 -1 0; -1 4 -1; 0 -1 0];
D2I=conv2(I2,kL,'same');
umbral=0.0001;
ind=find(abs(D2I)<umbral);
Z=ones(size(I2));
Z(ind)=0;
dibuja_contornos(I,Z,0)

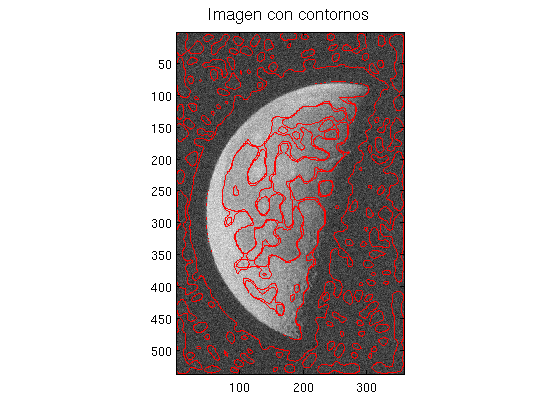
Paso 4. Observar que, debido al ruido, aparecen bordes incorrectos fuera de la luna. En este caso particular, se pueden eliminar facilmente con el método del valor umbral en la imagen desenfocada.

I2=I2.*(I2>0.5);

y volvemos a aplicar el Paso 3.

kL=[0 -1 0; -1 4 -1; 0 -1 0];
D2I=conv2(I2,kL,'same');
umbral=0.0001;
ind=find(abs(D2I)<umbral);
Z=ones(size(I2));
Z(ind)=0;
dibuja_contornos(I,Z,0)

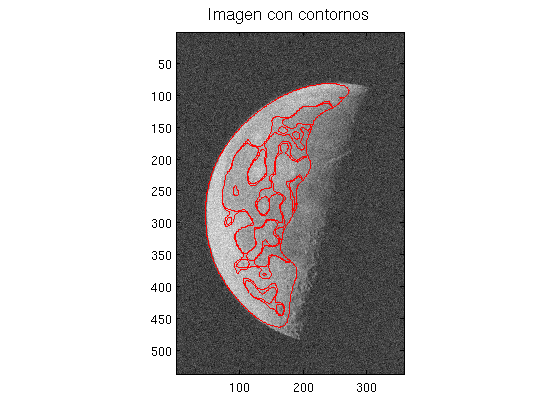
Ejercicio 2. Vamos a realizar un análisis similar pero usando un kernel basado en el gradiente: \[ DI=\sqrt{(DxI)^2+(DyI)^2}\] donde \(DxI\) and \(DyI\) se calculan mediante una convolución del la imagen con los kernels \[kx=0.5\left(\begin{array}{rrr} 0 & 0 & 0 \\-1 & 0 & 1 \\0 & 0 & 0 \end{array}\right) \quad\quad\quad ky=0.5\left(\begin{array}{rrr} 0 & -1 & 0 \\0 & 0 & 0 \\0 & 1 & 0 \end{array}\right) \]

Repetir los pasos anteriores introduciendo los cambios:

Cargar la imagen de Matlab coins.png y usar ruido=0.5.
Variar el número de iteraciones del Paso 2, y visulizar los resultados para comprender cómo funciona el filtro de desenfoque.
En el Paso 3, construir el filtro \(DI\). En este caso, usar umbral=0.01.
Usar la imagen desenfocada en el Paso 4.

Ejercicio2