Numerical differentiation¶
Contents¶
First order derivatives¶
We seek for approximating $f'$ in $\hat x \in [a,b]\subset \mathbb{R}$ that depends only on values of $f$ in a finite number of points close to $\hat x$.
The two main reasons to do this are:
- We only know the value of $f$ in some points $x$.
- It is cheaper to compute the approximation than the exact value.
The derivative of a function $f$ in $\hat x$ can be defined
$$ f'(\hat x)=\lim_{h\to0}\frac{f(\hat x+h)-f(\hat x)}{h} $$The following approximations or finite differences schemes can be obtained
Forward
$$ (\delta^+ f)(\hat x)=\frac{f(\hat x+h)-f(\hat x)}{h}$$Backward
$$ (\delta^- f)(\hat x)=\frac{f(\hat x)-f(\hat x -h)}{h}$$Centered
$$ (\delta f)(\hat x)=\frac{1}{2}\big((\delta^+ f)(\hat x)+(\delta^- f)(\hat x)\big)= \frac{f(\hat x+h)-f(\hat x-h)}{2h}$$For all the above schemes, the edge problem arises, due to the fact that the finite differences cannot be computed at one or both of the interval borders. For instance, if the forward formula is used we cannot compute $(\delta^+f)(b)$ because we need $f(b+h)$ that, in general, it is unknown.
Python commands
The following commands can be useful in the exercises: np.diff(x) that computes the vector $(x_2-x_1,x_3-x_2,\ldots,x_n-x_{n-1})$ for the $n-$dimensional vector $(x_1,x_2,\ldots,x_n)$, and np.linalg.norm(x) that computes the euclidean norm of a vector $x$
For the function $f(x)=e^x$ in $[h,1-h]$ and for h=0.1 and h=0.01.
- Compute and plot its exact derivative in the interval $[h,1-h]$.
- Compute and plot, on the previous figure and in the same interval, its approximate derivative, using finite differences, forward
df_f, backwarddf_band centereddf_c. - In a new figure, plot the absolute error for each approximation for each point.
- Using the
np.linalg.norm(x)command, compute the global relative error for each approximation:
%matplotlib inline
from __future__ import division
import numpy as np
import matplotlib.pyplot as plt
%run Exercise1.py
We see that the centered scheme gives better results. That is because forward and backward formulas are order 1 formulas and the centered formula is an order 2 formula.
Is it possible to get order 2 approximations for $f'a)$ and $f'(b)$? If we use a Lagrange interpolation polinomial of $f$ of second degree in $x_0$, $x_1$, $x_2$, with $y_j=f(x_j)$.
$$ p(x)=[y_{0}]+[y_{0},y_{1}](x-x_{0})+[y_{0},y_{1},y_{2}](x-x_{0})(x-x_{1}) $$We have
$$ [y_{0}]=y_{0},\quad[y_{0},y_{1}]=\frac{y_{1}-y_{0}}{x_{1}-x_{0}}=\frac{y_{1}-y_{0}}{h}, $$$$ [y_{0},y_{1},y_{2}]=\frac{[y_{1},y_{2}]-[y_{0},y_{1}]}{x_{2}-x_{0}}=\frac{1}{2h}\big(\frac{y_{2}-y_{1}}{h}-\frac{y_{1}-y_{0}}{h}\big)=\frac{1}{2h^{2}}\big(y_{0}-2y_{1}+y_{2}\big). $$$$ [y_{0}]=y_{0},\quad[y_{0},y_{1}]=\frac{y_{1}-y_{0}}{h},\quad[y_{0},y_{1},y_{2}]=\frac{1}{2h^{2}}(y_{0}-2y_{1}+y_{2}). $$If we differentiate $p(x)$
$$ f'(x)\approx p'(x)=[y_{0},y_{1}]+[y_{0},y_{1},y_{2}]((x-x_{0})+(x-x_{1})), $$If we substitute $x$ for $x_0$ we obtain an order 2 forward formula
$$ f'(x_{0})\approx p'(x_{0})=[y_{0},y_{1}]+[y_{0},y_{1},y_{2}]((x_{0}-x_{0})+(x_{0}-x_{1})), $$$$ f'(x_{0})\approx\frac{y_{1}-y_{0}}{h}+\frac{1}{2h^{2}}\big(y_{0}-2y_{1}+y_{2}\big)(-h), $$$$ f'(x_{0})\approx\frac{-3y_{0}+4y_{1}-y_{2}}{2h}. $$If we substitute $x$ for $x_1$, we obtain an order 2 centered formula we already had
$$ f'(x_{0})\approx p'(x_{0})=[y_{0},y_{1}]+[y_{0},y_{1},y_{2}]((x_{0}-x_{0})+(x_{0}-x_{1})), $$$$ f'(x_{0})\approx\frac{y_{1}-y_{0}}{h}+\frac{1}{2h^{2}}\big(y_{0}-2y_{1}+y_{2}\big)(-h), $$$$ f'(x_{0})\approx\frac{-3y_{0}+4y_{1}-y_{2}}{2h}. $$and substituting $x$ for $x_2$ we obtain an order 2 backward formula
$$ f'(x_{2})\approx p'(x_{2})=[y_{0},y_{1}]+[y_{0},y_{1},y_{2}]((x_{2}-x_{0})+(x_{2}-x_{1})), $$$$ f'(x_{2})\approx\frac{y_{1}-y_{0}}{h}+\frac{1}{2h^{2}}\big(y_{0}-2y_{1}+y_{2}\big)(2h+h), $$$$ f'(x_{2})\approx\frac{y_{0}-4y_{1}+3y_{2}}{2h}. $$They also can be written:
$$ \begin{array}{l} \mathbf{Forward}\\ f'(\hat x)\approx \frac{1}{2h}(-3f(\hat x)+4f(\hat x+h)-f(\hat x+2h))\\ \mathbf{Centered}\\ f'(\hat x)\approx \frac{1}{2h}(f(\hat x+h)-f(\hat x-h))\\ \mathbf{Backward}\\ f'(\hat x)\approx \frac{1}{2h}(f(\hat x-2h)-4f(\hat x-h)+3f(\hat x)) \end{array} $$For the function $f(x)=\dfrac{1}{x}$ in $[0.2,1.2]$, and h=0.01.
- Compute its approximate derivative in the interval $[0.2,1.2]$ using the centered scheme for the interior points and forward and backward schemes on $x=0.2$ and $x=1.2$, respectively.
- Compute the approximate derivative by using a centered scheme in the interior points and the order 2 formulas deduced for $x=0.2$ and $x=1.2$, respectively.
- Compute the exact derivative in the interval $[0.2,1.2]$, and then the global relative error of each approximation.
%run Exercise2.py
Second order derivatives¶
From the interpolating polynomial
$$ p(x)=[y_1]+[y_1,y_2](x-x_1)+[y_1,y_2,y_3](x-x_1)(x-x_2) $$we obtain
$$p''(x_2)=2[y_1,y_2,y_3]= \frac{1}{h^2}(y_1-2y_2+y_3)\quad (1)$$For $f(x)=\sin(2\pi x)$ in $[0,1]$ and h=0.01:
Compute the exact second derivative, the approximate second derivative according to formula (1) and the relative error of the approximation in the interval $[h,1-h]$.
%run Exercise3.py
Numerical differentiation of functions of several variables¶
For $\Omega =[a,b]\times[c,d]\subset \mathbb{R}^2$, consider uniform partitions
\begin{eqnarray*} a=x_1 \lt x_2 \lt \ldots \lt x_{M-1} \lt x_M=b \\ c=y_1 \lt y_2 \lt \ldots \lt y_{N-1} \lt y_N=d \end{eqnarray*}Denote a point by $(x_m,y_n)$. Then, its neighbor points are
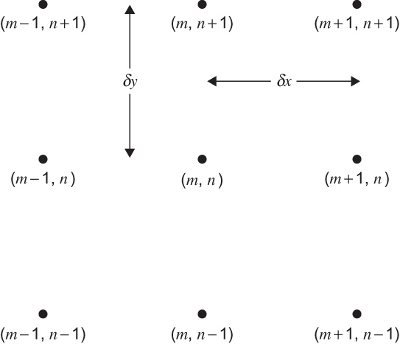
We may use the same ideas than those used for scalar functions. For instance
- x-partial derivative (forward):
$\partial_x f(x_m,y_n)$
$$ (\delta_x^+f)(x_m,y_n)= \frac{f(x_{m+1},y_n)-f(x_{m},y_n)}{h_x} $$- Gradient (centered):
$\nabla f(x_m,y_n)=(\partial_x f(x_m,y_n),\partial_y f(x_m,y_n))$
$$ \left(\frac{f(x_{m+1},y_n)-f(x_{m-1},y_n)}{2h_x}, \frac{f(x_{m},y_{n+1})-f(x_{m},y_{n-1})}{2h_y}\right)\quad (2) $$- Divergence (centered):
$\mathrm{div} (\mathbb{f}(x_m,y_n))=\partial_x f_1(x_m,y_n)+\partial_y f_2(x_m,y_n)$
$$ \frac{f_1(x_{m+1},y_n)-f_1(x_{m-1},y_n)}{2h_x}+ \frac{f_2(x_{m},y_{n+1})-f_2(x_{m},y_{n-1})}{2h_y} \quad (3) $$- Laplacian (centered):
$\Delta f(x_m,y_n)=\partial_{xx} f(x_m,y_n)+ \partial_{yy} f(x_m,y_n)$
$$ \frac{f(x_{m+1},y_n)-2f(x_m,y_n)+f(x_{m-1},y_n)}{h_x^2}+ \frac{f(x_{m},y_{n+1})-2f(x_m,y_n)+f(x_{m},y_{n-1})}{h_y^2} \quad (4) $$Before entering into matter, let us recall the basics on plotting surfaces and vector functions with python.
We will represent the functions in rectangular domains. We decide how many points we use in the representation.
We import some modules
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.cm as cm
from mpl_toolkits.mplot3d import Axes3D
If we want to plot the escalar function $f(x,y)=-x^2-y^2$ in $x \in [0,5]$ with step $h_x=1$ and $y \in [-2,2]$ with step $h_y=1$, first we create a grid
h = 1.
x = np.arange(0., 5. + h, h)
y = np.arange(-2., 2. + h, h)
x, y = np.meshgrid(x, y)
In this way we have generated two matrices with the components of the coordinates of the given domain
print(x)
print(y)
Now, we may compute the values of $z=f(x,y)=-x^2-y^2$ for each pair $(x_{ij},y_{ij}) \quad i=1,\ldots,m,\,j=1,\ldots,n$ being $m$ and $n$ the number of rows and columns of x and y. Performing the operations element-wise, we obtain a $m\times n$ matrix z
z = -(x**2 + y**2)
print(z)
With these matrices x, y, z we have all what we need to plot $f$.
fig = plt.figure(figsize=(10,6))
ax = fig.add_subplot(221, projection='3d')
ax.plot_surface(x, y, z, rstride=1, cstride=1, linewidth=0,
cmap=cm.coolwarm)
ax = fig.add_subplot(222, projection='3d')
ax.plot_wireframe(x, y, z)
ax = fig.add_subplot(223)
plt.contour(x, y, z)
ax = fig.add_subplot(224)
plt.contourf(x, y, z)
plt.colorbar();
plt.suptitle(r'$f(x,y)=-x^2-y^2$', fontsize=20);
For plotting a vector function $\mathbb{f}=(f_1(x,y),f_2(x,y))$ we use quiver
f1 = lambda x, y: (x**2 + y**2)/3
f2 = lambda x, y: (x**2 - y**2)/2
plt.figure()
ax = plt.gca()
ax.quiver(x,y,f1(x,y),f2(x,y))
ax.set_xlim([-1,6])
ax.set_ylim([-3,3]);
The numpy command
fy, fx = np.gradient(f,hx,hy)
returns the gradient (numerically computed) of the real function $f$. The input f is the matrix of the values of $f$ in the points of a grid created with steps hx and hy. The output fx and fy are two matrices of the same dimension as f that contains the coordinates of the gradient for each point of the grid. The function uses a order 2 centered schema for the interior points and order one or two differences, forward or backward at the edges.
%run Exercise4.py
- Compute the divergence of $\mathbb{f}(x,y)=(f_1(x,y),f_2(x,y))=(x^2+y^2,x^2-y^2)$ in $[-2,2]\times[-2,2]$ using the outputs of
gradientfor the functions $f_1$ y $f_2$, withhx=0.1andhy=0.1. Plot $\mathbb{f}$ y $\text{div} (\mathbb{f})$ in the same figure. - A boundary effect may be noticed in these plots due to the bad approximation of the divergence on these points.
- Se aprecia un efecto en los bordes debido a una mala aproximación de la divergencia en estos puntos. Remake the plots above restricting the set to $[-2+h_x,2-h_x]\times[-2+h_y,2-h_y]$.
- Compute the global relative errors of the approximation in both sets using
np.linalg.norm.
%run Exercise5.py
%run Exercise6.py