The Lie algebra $\mathfrak{g}_{2(+2)}$ written in a symplectic manner
First of all, let me point out that I think this is nothing new nor special: I decided to
write it down as when I needed it, I googled a few hours, decided that it was probably
better to sort out the details myself and thought that maybe it could be of some help to someone
at some point.
For some nice information on $G_{2}$ see for instance I. Yokota's Exceptional Lie groups or
N.J. Wilberger's An easy construction of G2. Of course this isn't by
any means an exhaustive list. On the contrary: it is an infinitesimal list!
Here we go: $\mathfrak{g}_{2(+2)}$ is a real form of the exceptional simple Lie algebra
G2, with 6 compact and 8 non-compact generators. According to LiE it has a
$\mathfrak{sp}(1;\mathbb{R})\oplus\mathfrak{sp}(1;\mathbb{R})$ subalgebra, under which $\mathfrak{g}_{2(+2)}$'s adjoint branches as
$\mathbf{14}\rightarrow (\mathbf{3},\mathbf{1})\oplus (\mathbf{1},\mathbf{3})\oplus (\mathbf{2},\mathbf{4})$.
Now, $\mathbf{3}$ is $\mathfrak{sp}(1;\mathbb{R})$'s adjoint representation, $\mathbf{2}$ is its vector representation and $\mathbf{1}$ is clearly the singlet.
Let us denote the anti-Hermitean generators of one $\mathfrak{sp}(1;\mathbb{R})$ by $S_{\alpha\beta}$ ($=S_{\beta\alpha}=-S^{\dagger}_{\alpha\beta}$; $\alpha ,\beta =0,1$)
and the ones to the other one by $R_{AB}$ ($=R_{BA}=-R^{\dagger}_{AB}$; $A ,B =0,1$). Since we are dealing with symplectic stuff, we define the symplectic metrics
\begin{equation}
\varepsilon_{01}\ =\ \varepsilon^{01}\ =\ 1 \;\;\;\mbox{whence}\;\;\;
\varepsilon_{AC}\varepsilon^{BC}\ =\ \delta_{A}{}^{C} \;\;\mbox{and}\;\;
\varepsilon_{\alpha\gamma}\varepsilon^{\beta\gamma}\; =\; \delta_{\alpha}{}^{\beta} \; .
\end{equation}
And of course, since the symplectic metric is anti-symmetric I need to specify the rules to raise and lower indices with them: for no obvious
reason I choose
\begin{equation}
V_{A}\; \equiv\; \varepsilon_{AB}\ V^{B} \;\;\; ,\;\;\;
V^{A}\; \equiv\; V_{B}\ \varepsilon^{BA} \; ,
\end{equation}
and similar for the greek indices.
With these definitions we can then take the $\mathfrak{sp}(1;\mathbb{R})$ commutation relations to be
\begin{eqnarray}
\left[\ S_{\alpha\beta}\ ,\ S_{\gamma\delta}\ \right] \; =\; 2\varepsilon_{\alpha (\gamma}\ S_{\delta )\beta} \ +\ 2\varepsilon_{\beta (\gamma}\ S_{\delta )\alpha} \; , \\
\left[\ R_{AB}\ ,\ R_{CD}\ \right] \; =\; 2\varepsilon_{A(C}\ R_{D)B} \ +\ 2\varepsilon_{B(C}\ R_{D)A} \; ,
\end{eqnarray}
As indicated by the above branching rule, we are still missing a set of generators transforming as the $(\mathbf{2},\mathbf{4})$ under the
$\mathfrak{sp}(1;\mathbb{R})\oplus\mathfrak{sp}(1;\mathbb{R})$ subalgebra: in fact it is easy to see that they can be written as $T_{\alpha ABC}$
which is totally symmetric in the $ABC$-indices, and therefore we automatically have
\begin{eqnarray}
\left[\ S_{\alpha\beta}\ ,\ T_{\gamma ABC}\ \right] & =& \varepsilon_{\alpha \gamma}\ T_{\beta ABC}\ +\ \varepsilon_{\beta\gamma}\ T_{\alpha ABC} \; , \\
\left[\ R_{AB}\ ,\ T_{\alpha C_{1}C_{2}C_{3}}\ \right] & =& 3\ \varepsilon_{A(C_{1}|}\ T_{\alpha |C_{2}\cdots C_{3})B}
\ +\ 3\ \varepsilon_{B(C_{1}|}\ T_{\alpha |C_{2}\cdots C_{3})A} \; .
\end{eqnarray}
The remaining commutation relations are then
\begin{equation}
\left[\ T_{\alpha ABC}\ ,\ T_{\beta}{}^{DEF}\ \right] \; =\;
\varepsilon_{\alpha\beta}\ \delta_{(A}{}^{(D}\delta_{B}{}^{E}\ R_{C)}{}^{F)}
\ -\ \delta_{(A}{}^{(D}\delta_{B}{}^{E}\delta_{C)}{}^{F)}\ S_{\alpha\beta} \; .
\end{equation}
If you like the assignments of the operators w.r.t. the perhaps more familiar root system is such that
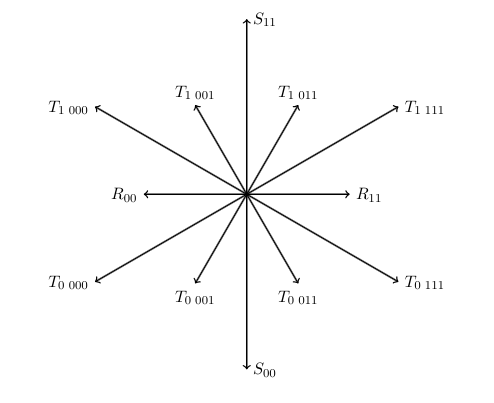
and the Cartan subalgebra is spanned by $S_{01}$ and $R_{01}$.
The quadratic Casimir operator is then compactly written as
\begin{equation}
\mathcal{C}_{(2)}\; =\; \textstyle{1\over 2}\ S_{\alpha\beta}\otimes S^{\alpha\beta}
\ +\ \textstyle{1\over 6}\ R_{AB}\otimes R^{AB}
\ +\ T_{\alpha ABC}\otimes T^{\alpha ABC} \; ,
\end{equation}
which when written out has 6 generators that carry a minus sign and 8 that carry a plus sign,
which is the correct one for $\mathfrak{g}_{2(+2)}$.
Last modified: Thu Mar 19 12:54:41 CET 2015

